5 Estructuras de datos

Hasta ahora todos los algoritmos que hemos desarrollado hacen uso de objetos que guardan datos individuales, los cuales representan un número, una cadena de texto o un valor lógico. Sin embargo, la verdadera utilidad de la computación radica en poder trabajar con conjuntos de datos, organizados de acuerdo a ciertas reglas que permitan su manipulación y acceso. Definimos entonces como estructura de datos a un conjunto de datos que cuentan con un sistema de organización.

5.1 Arreglos

Un arreglo se define como una colección de valores individuales con dos características fundamentales:

Ordenamiento: los valores individuales pueden ser enumerados en orden, es decir, debe ser posible identificar en qué posición del arreglo se encuentra cada valor.
Homogeneidad: los valores individuales almacenados en un arreglo son todos del mismo tipo (numérico, carácter, lógico).

Los arreglos son muy útiles para almacenar información en la memoria de la computadora, organizando valores que estén relacionados entre sí de alguna manera, por ejemplo, una conjunto de precios, los meses del año, el listado de calificaciones de estudiantes en distintos parciales, etc.

Los componentes individuales del conjunto se llaman elementos. Para indicar qué posición ocupa cada elemento en el arreglo se emplean uno o más índices. Dependiendo de cuántos índices se deban utilizar para acceder a cada elemento dentro de los arreglos, estos se clasifican en unidimensionales (vectores) o bidimensionales (matrices). También existen los arreglos multidimensionales y están presentados al final de este capítulo, pero como no trabajaremos la lectura de esa sección es opcional.

5.1.1 Arreglos unidimensionales o vectores

Un arreglo unidimensional o vector tiene n elementos todos del mismo tipo. Por ejemplo, el siguiente es un vector de tipo numérico llamado x con 5 elementos:

Figura 5.1: Ejemplo de un vector numérico

Cada uno de los elementos ocupa una posición determinada en el vector. Por ejemplo, el elemento 3 del vector x es el numéro 2.71. Se puede acceder o hacer referencia a cada elemento mediante el uso de índices, expresados entre corchetes al lado del nombre del vector. De esta forma, si escribimos x[3] hacemos referencia a la tercera posición del vector, que actualmente guarda al valor 2.71. Como podemos ver, sólo hace falta un índice para hacer referencia a cada elemento de un vector.

Figura 5.2: Ejemplo de un vector numérico: índices para señalar cada posición.

Los siguientes son ejemplos de vectores de tipo carácter y lógico, con distintas cantidades de elementos:

Figura 5.3: Ejemplo de un vector carácter y un vector lógico

Al igual que todas las variables que empleamos en nuestros algoritmos, los vectores que serán utilizados deben ser declarados en el pseudocódigo, eligiendo un identificador (nombre) e indicando su tipo y su tamaño, es decir, la cantidad de posiciones que contienen. Esto último se señala entre paréntesis al lado del nombre elegido. Por ejemplo, el vector x visto anteriomente puede ser creado de la siguiente forma:

VARIABLE numérica x(5)
x[1] <- -4.5
x[2] <- 12
x[3] <- 2.71
x[4] <- -6
x[5] <- 25

Si bien la declaración de un vector sólo tiene como objetivo permitirle a la computadora que reserve internamente el espacio necesario en memoria para el mismo, para escribir pseudocódigo de una manera sencilla estableceremos la siguiente convención. Cuando declaramos un vector de tipo numérico con la expresión VARIABLE numérica x(5) asumiremos que, además de reservar espacio en memoria para el vector, se le asigna un 0 (cero) en cada posición. Es decir, el vector x es iniciado con ceros, que más tarde pueden ser reemplazados por otros valores. Del mismo modo, asumiremos que cuando declaramos vectores de tipo carácter, todos sus elementos son iniciados con valores "" (una cadena de texto vacía) y cuando declaramos vectores de tipo lógico, con el valor FALSO.

En R, los vectores se construyen de forma dinámica por lo cual no es necesario declararlos antes de comenzar a utilizarlos. La función c() (de combinar) permite crear vectores, por ejemplo, los mencionados anteriormente:

x <- c(-4.5, 12, 2.71, -6, 25)
y <- c("ARG", "correo@gmail.com", "Ok", "chau")
z <- c(TRUE, TRUE, FALSE)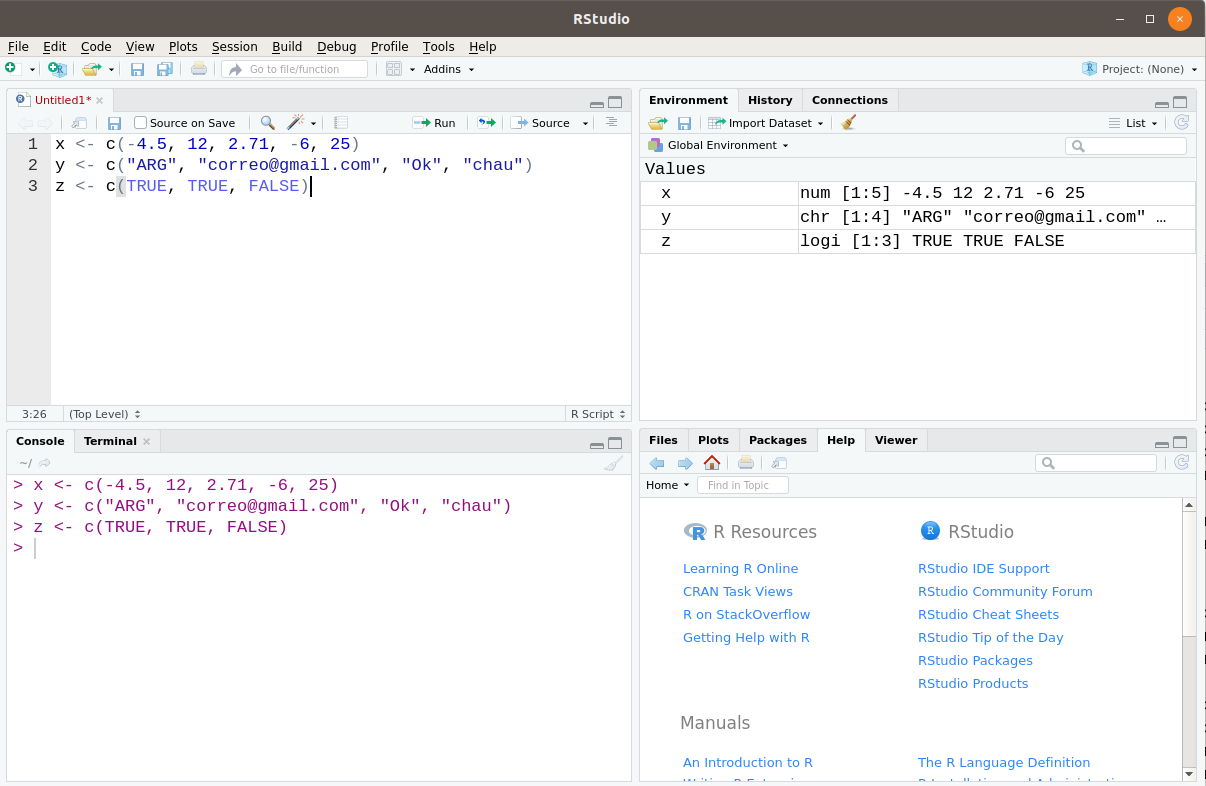

Figura 5.4: Creación de vectores en R

Cuando ejecutamos dichas líneas, se crean en el ambiente global los objetos x, y y z, como podemos notar en la pestaña Environment de RStudio. Es decir, los vectores, así como cualquier otro tipo de arreglo, son objetos que constituyen entidades en sí mismas y que pueden ser manipulados al hacer referencia a sus indicadores. Además, RStudio nos muestra en la pestaña mencionada qué tipo de vector es cada uno (num, chr, logi), cuántos elementos tiene ([1:5], [1:4], [1:3]) y una previsualización de sus primeros elementos.

Dado que la función c() resulta, en consecuencia, muy importante al programar en R, es recomendable que evitemos usar la letra c como nombre para otros objetos²².

Podemos emplear estructuras iterativas para recorrer todas las posiciones de un vector y realizar operaciones con ellas, por ejemplo:

PARA i DESDE 1 HASTA 5 HACER
    ESCRIBIR "La posición " i "de x está ocupada por el valor " x[i]
FIN PARA

for (i in 1:5) {
    cat("La posición", i, "de x está ocupada por el valor", x[i], "\n")
}

La posición 1 de x está ocupada por el valor -4.5 
La posición 2 de x está ocupada por el valor 12 
La posición 3 de x está ocupada por el valor 2.71 
La posición 4 de x está ocupada por el valor -6 
La posición 5 de x está ocupada por el valor 25

Todos los lenguajes de programación incluyen, además, alguna función para determinar cuántos elementos tiene un vector que ya fue creado. Para esto emplearemos la expresión LARGO() en el pseudocódigo y la función length de R:

ESCRIBIR "El vector x tiene " LARGO(x) " elementos."
ESCRIBIR "El vector y tiene " LARGO(y) " elementos."
ESCRIBIR "El vector z tiene " LARGO(z) " elementos."

cat("El vector x tiene", length(x), "elementos.")

El vector x tiene 5 elementos.

cat("El vector y tiene", length(y), "elementos.")

El vector y tiene 4 elementos.

cat("El vector z tiene", length(z), "elementos.")

El vector z tiene 3 elementos.

Entonces, para recorrer todos los elementos del vector podemos hacer también:

PARA i DESDE 1 HASTA LARGO(x) HACER
    ESCRIBIR "La posición " i "de x está ocupada por el valor " x[i]
FIN PARA

O bien:

tam <- LARGO(x)
PARA i DESDE 1 HASTA tam HACER
    ESCRIBIR "La posición " i "de x está ocupada por el valor " x[i]
FIN PARA

Antes comentamos que en R los vectores se crean con expresiones como x <- c(-4.5, 12, 2.71, -6, 25), donde sus elementos están listados de forma literal. También podemos crear vectores de un largo determinado dejando que cada posición quede ocupada por algún valor asignado por defecto. Por ejemplo, el siguiente código crea un vector tipo numérico con 10 posiciones, uno carácter con 7 y otro lógico con 2. En cada caso, R rellena todas las posiciones con el mismo valor: ceros en el vector numérico, caracteres vacíos "" en el vector de tipo carácter y valores FALSE en el vector lógico:

a <- numeric(10)
b <- character(7)
d <- logical(2)

a

 [1] 0 0 0 0 0 0 0 0 0 0

[1] "" "" "" "" "" "" ""

[1] FALSE FALSE

Se pueden asignar valores a una, varias o todas las posiciones de un vector en cualquier parte del algoritmo. Además, en pseudocódigo emplearemos la palabra clave MOSTRAR cuando deseamos que se escriba en pantalla todo el contenido de un vector. Por ejemplo:

VARIABLE numérica a(10)
PARA i DESDE 1 HASTA LARGO(a) HACER
    SI i MOD 3 == 0 ENTONCES  
        a[i] <- i * 100
    FIN SI
FIN PARA
MOSTRAR a

a <- numeric(10)
for (i in 1:length(a)) {
    if (i %% 3 == 0) {
        a[i] <- i * 100
    }
}
a

 [1]   0   0 300   0   0 600   0   0 900   0

En los ejemplos anteriores, declaramos los vectores explicitando su tamaño con un número: VARIABLE numérica x(5) o VARIABLE numérica a(10). Sin embargo, el tamaño del vector podría estar guardado en otra variable, cuyo valor se determina en cada ejecución del programa mediante información externa o como resultado de algún cálculo anterior. En el siguiente ejemplo se deja que el usuario determine la dimensión del vector y que provea cada uno de los valores para el mismo. Antes de poder declarar la existencia del nuevo vector llamado mi_vector, se “lee” su tamaño:

VARIABLE numérica tam
LEER tam
VARIABLE numérica mi_vector(tam)
PARA i DESDE 1 HASTA tam HACER
    LEER mi_vector[i]
FIN PARA

Por ahora, toda instrucción de leer en el pseudocódigo será traducida en R mediante la asignación directa de valores. Por ejemplo, LEER tam se reemplaza por tam <- 5 (o el número que necesitemos).

Antes de terminar esta sección haremos una última observación. En R todos los objetos que hemos considerado como “variable” y que guardan un único valor (como tam en el ejemplo anterior), son también considerados como vectores, cuyo largo es 1, como podemos verificar en el siguiente ejemplo:

x <- 25
length(x)

[1] 1

is.vector(x) # Esta función lógica le pregunta a R si el objeto x es un vector

[1] TRUE

Ejemplo: invertir los elementos de un vector

Nos planteamos el problema de dar vuelta los elementos pertenecientes a un vector, de manera que el primer elemento pase a ser el último, el segundo pase al penúltimo lugar, etcétera. Por ejemplo, dado el vector de tipo carácter v:

Figura 5.5: Vector v original

queremos modificarlo para obtener:

Figura 5.6: Vector v reordenado

Si bien podemos pensar en distintas formas para resolver este problema, probablemente la más sencilla requiere que intercambiemos de a dos los valores en ciertas posiciones del vector, por ejemplo, empezando por intercambiar el primero con el último. Para esto podemos emplear una variable auxiliar que guarde el valor de alguna de las celdas temporariamente (por eso lo vamos a llamar tmp):

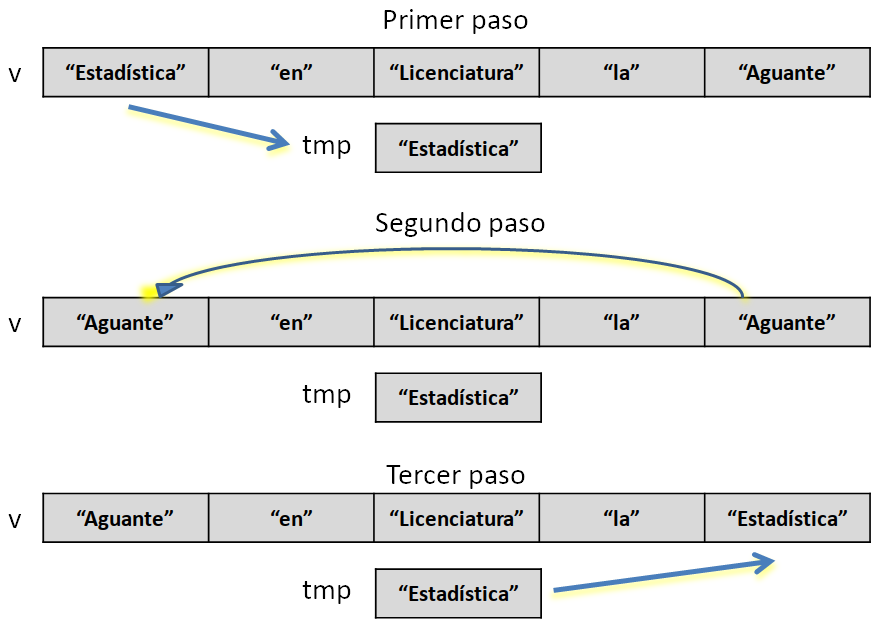
Figura 5.7: Pasos para intercambiar valores

Ahora sólo resta realizar el mismo procedimiento para los valores de las posiciones 2 y 4. Como el número de elementos en el vector es impar, el valor en la posición central queda en su lugar. Podemos definir el siguiente algoritmo para resolver este problema de manera general. En el siguiente pseudocódigo, primero declaramos una variable numérica n que puede tomar cualquier valor y que servirá para declarar cuántos espacios necesita el vector. Luego, se itera para leer cada elemento del vector. Finalmente, se implementa la estrategia de reordenamiento:

ALGORITMO: "Invertir (dar vuelta) los elementos de un vector"
COMENZAR
    
  # Declarar variables
  VARIABLE numérica n
  VARIABLE carácter tmp
  LEER n
  VARIABLE carácter v(n)
  
  # Asignar valores al vector
  PARA i DESDE 1 HASTA n HACER
      LEER v[i]
  FIN PARA
  
  # Reordenar
  PARA i DESDE 1 HASTA n DIV 2 HACER
      tmp <- v[i]                 # Paso 1
      v[i] <- v[n - i + 1]        # Paso 2
      v[n - i + 1] <- tmp         # Paso 3
  FIN PARA
  
  # Mostrar el vector reodenado
  MOSTRAR v
    
FIN

En el ejemplo anterior hemos incorporado el uso de comentarios en el pseudocódigo para describir el objetivo de cada parte. Imitando lo que hacemos en R, señalamos la presencia de comentarios con el carácter # (podríamos usar otra cosa, pero adheriremos a esta convención). Se usó el operador DIV para obtener la división entera entre n y 2 (por ejemplo, 5 DIV 2 = 2). En R reemplazamos todas las instrucciones LEER por una asignación directa de valores y empleamos el operador de división entera %/%:

v <- c("Estadística", "en", "Licenciatura", "la", "Aguante")
n <- length(v)
for (i in 1:(n%/%2)) {
    tmp <- v[i]
    v[i] <- v[n - i + 1]
    v[n - i + 1] <- tmp
}
v

[1] "Aguante"      "la"           "Licenciatura" "en"           "Estadística"

5.1.2 Arreglos bidimensionales o matrices

Un arreglo bidimensional representa lo que habitualmente conocemos en matemática como matriz y por eso también lo llamamos de esa forma. Podemos imaginar que en una matriz los elementos están organizados en filas y columnas formando una tabla. Por ejemplo, la siguiente es una matriz llamada x:

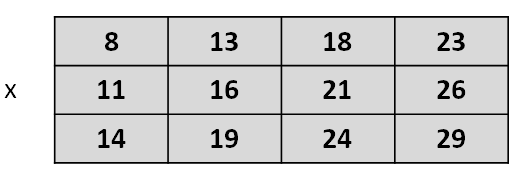
Figura 5.8: Ejemplo de una matriz numérica

A diferencia de los vectores, las matrices requieren dos índices para señalar la posición de cada elemento, el primero para indicar la fila y el segundo para indicar la columna. Los mismos se colocan entre corchetes, separados por una coma, al lado del identificador de la matriz. De esta forma, si hablamos de x[1, 3] hacemos referencia a la posición ocupada por el valor 18, mientras que si mencionamos x[3, 1] nos referimos al valor 14.

Figura 5.9: Ejemplo de una matriz numérica: índices para señalar cada posición

Al tamaño de una matriz, es decir, cuántas filas y columnas tiene, se le dice dimensión. La matriz anterior es de dimension \(3 \times 4\).

Como hicimos con los vectores, debemos declarar las matrices que vamos a usar en el pseudocódigo, indicando su identificador, tipo y dimensión: VARIABLE numérica x(3, 4). También vamos a asumir que todas las posiciones de una matriz son iniciadas con el valor 0, "" o FALSO si la misma es numérica, carácter o lógica, respectivamente. La matriz x puede ser generada en pseudocódigo de esta forma:

VARIABLE numérica x(3, 4)
x[1, 1] <- 8
x[1, 2] <- 13
x[1, 3] <- 18
x[1, 4] <- 23
x[2, 1] <- 11
x[2, 2] <- 16
x[2, 3] <- 21
x[2, 4] <- 26
x[3, 1] <- 14
x[3, 2] <- 19
x[3, 3] <- 24
x[3, 4] <- 29

En R, no es necesario declarar las matrices con anterioridad y las mismas pueden ser creadas de manera literal con la función matrix(). Su primer argumento, data, es un vector con todos los elementos que queremos guardar en la matriz. Luego, se indica la cantidad de filas para la misma con nrow y la cantidad de columnas con ncol:

x <- matrix(data = c(8, 11, 14, 13, 16, 19, 18, 21, 24, 23, 26, 29),
            nrow = 3, ncol = 4)
x

     [,1] [,2] [,3] [,4]
[1,]    8   13   18   23
[2,]   11   16   21   26
[3,]   14   19   24   29

Notar que R ubicó a los valores provistos llenando primero la columna 1, luego la 2, etc. Ese comportamiento puede ser modificado con el argumento byrow, que por default es FALSE. Si lo cambiamos a TRUE los elementos son ubicados por fila. Además, podemos usar saltos de líneas (enter) para visualizar las diferentes filas de la matriz. Esto no tiene ningún impacto en R, sólo sirve para que el código sea más fácil de leer. Dado que hemos provisto 12 valores e indicamos que queremos 3 filas, el argumento ncol no es necesario (es obvio que quedarán 4 columnas). Por eso, las siguientes sentencias son equivalentes a la anterior:

x <- matrix(c( 8, 13, 18, 23, 
              11, 16, 21, 26, 
              14, 19, 24, 29), 
            nrow = 3, byrow = TRUE)

x <- matrix(c( 8, 13, 18, 23, 
              11, 16, 21, 26, 
              14, 19, 24, 29), 
            ncol = 4, byrow = TRUE)

Si colocamos un único valor como primer argumento en la función matrix(), el mismo se repetirá en todas las posiciones. En este caso sí o sí tenemos que indicar cuántas filas y columnas deseamos:

y <- matrix(0, nrow = 2, ncol = 5)
y

     [,1] [,2] [,3] [,4] [,5]
[1,]    0    0    0    0    0
[2,]    0    0    0    0    0

Una vez que la matriz ya existe, en el pseudocódigo haremos referencia al número de filas y columnas de la misma con las expresiones NFILA(x) y NCOL(x). En R tenemos las siguientes funciones para analizar el tamaño de las matrices:

dim(x)

[1] 3 4

nrow(x)

[1] 3

ncol(x)

[1] 4

dim(y)

[1] 2 5

nrow(y)

[1] 2

ncol(y)

[1] 5

Podemos recorrer todas las posiciones de una matriz con una estructura iterativa doble: nos situamos en la primera fila y recorremos cada columna, luego en la segunda fila y recorremos todas las columnas y así sucesivamente:

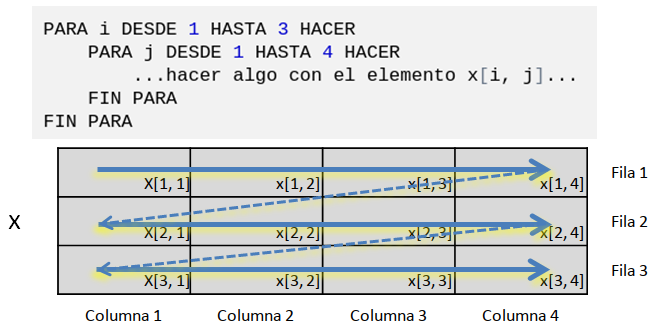
Figura 5.10: Recorrer una matriz por fila

También se puede recorrer la matriz por columna, si modificamos ligeramente las estructuras iterativas:

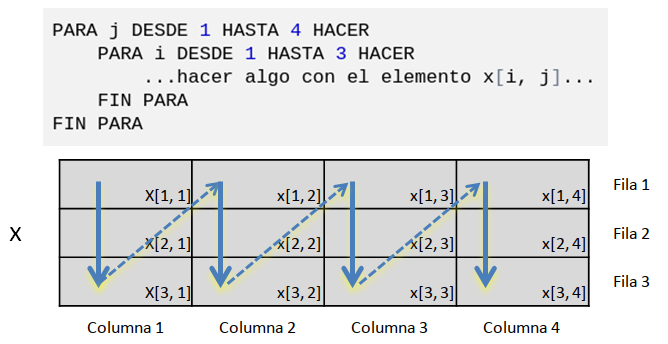
Figura 5.11: Recorrer una matriz por columna

Se puede usar cualquier letra o palabra como variables iteradoras, pero el uso de i para las filas y de j para las columnas es bastante común.

También podemos asignar valores en cada celda mientras recorremos la matriz. De hecho, la matriz x del ejemplo puede ser generada así, donde los índices i y j no sólo señalan una posición en particular dentro de la matriz, sino que además se usan para hacer el cálculo del valor a asignar:

VARIABLE numérica x(3, 4)
PARA i DESDE 1 HASTA NFILA(x) HACER
    PARA j DESDE 1 HASTA NCOL(x) HACER
        x[i, j] <- 3 * i + 5 * j
    FIN PARA
FIN PARA
MOSTRAR x

x <- matrix(0, nrow = 3, ncol = 4)
for (i in 1:nrow(x)) {
    for (j in 1:ncol(x)) {
        x[i, j] <- 3 * i + 5 * j
    }
}
x

     [,1] [,2] [,3] [,4]
[1,]    8   13   18   23
[2,]   11   16   21   26
[3,]   14   19   24   29

Si queremos dejar que el valor en cada posición sea determinado por una fuente de información externa a la hora de correr el programa, empleamos la sentencia LEER en el pseudocódigo:

VARIABLE numérica x(3, 4)
PARA i DESDE 1 HASTA NFILA(x) HACER
  PARA j DESDE 1 HASTA NCOL(x) HACER
    LEER x[i, j]
  FIN PARA
FIN PARA

Ejemplo: trasponer una matriz

En Álgebra, trasponer una matriz de dimensión \(m \times n\) significa generar una nueva matriz de dimensión \(n \times m\), donde los elementos se intercambian de este modo:

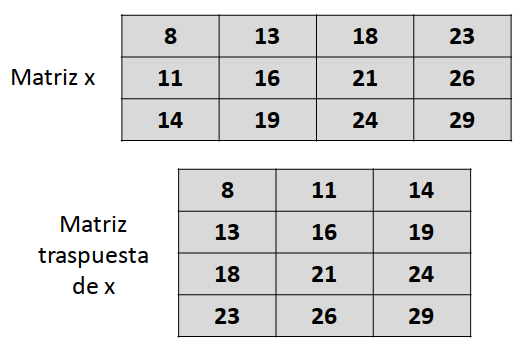
Figura 5.12: Matriz traspuesta

Podemos formalizar el algoritmo que permite generar la matriz traspuesta, teniendo en cuenta que cada elemento que originalmente ocupa la posición [i, j] en la matriz original, debe pasar a ocupar la posición [j, i] en la matriz traspuesta:

ALGORITMO: Trasponer matriz
COMENZAR
    
    # Declarar objetos
    VARIABLE numérica nf, nc
    LEER nf, nc
    VARIABLE numérica x(nf, nc), traspuesta(nc, nf)
    
    # Leer los valores de la matriz
    PARA i DESDE 1 HASTA nf HACER
        PARA j DESDE 1 HASTA nc HACER
            LEER x[i, j]
        FIN PARA
    FIN PARA
    
    # Trasponer
    PARA i DESDE 1 HASTA nf HACER
        PARA j DESDE 1 HASTA nc HACER
            traspuesta[j, i] <- x[i, j]
        FIN PARA
    FIN PARA
    
    # Mostrar ambas matrices
    ESCRIBIR "Matriz original"
    MOSTRAR x
    ESCRIBIR "Matriz traspuesta"
    MOSTRAR traspuesta
    
FIN

Dado que en R vamos a asignar valores en la matriz de manera literal, primero la creamos y luego usamos nrow() y ncol() para obtener los correspondientes valores de nf y nc. En el siguiente ejemplo, además, todas las posiciones de la matriz traspuesta son iniciadas con el valor NA.

x <- matrix(c( 8, 13, 18, 23, 
              11, 16, 21, 26, 
              14, 19, 24, 29), 
            nrow = 3, byrow = TRUE)
nf <- nrow(x)
nc <- ncol(x)
traspuesta <- matrix(NA, nc, nf)
for (i in 1:nf) {
    for (j in 1:nc) {
        traspuesta[j, i] <- x[i, j]
    }
}
cat("Matriz original\n")
x
cat("Matriz traspuesta\n")
traspuesta

Matriz original
     [,1] [,2] [,3] [,4]
[1,]    8   13   18   23
[2,]   11   16   21   26
[3,]   14   19   24   29
Matriz traspuesta
     [,1] [,2] [,3]
[1,]    8   11   14
[2,]   13   16   19
[3,]   18   21   24
[4,]   23   26   29

5.2 Características particulares de las estructuras de datos en R

Los vectores y matrices son estructuras que están bien representadas en casi cualquier lenguaje de programación. Por esta razón, ante diversos problemas computacionales podemos escribir algoritmos que empleando arreglos y operando con cada uno de sus elementos alcancen los objetivos propuestos.

No obstante, cada lenguaje de programación propone formas particulares de operar con los arreglos e incluso otros tipos de estructuras de datos. En esta sección nos dedicaremos a conocer cuáles son las herramientas que R nos ofrece para trabajar con vectores y matrices. Como son específicas de R, no hay convenciones generales para representarlas en pseudocódigo.

5.2.1 Elementos con nombre

Además de guardar información, los objetos de R pueden poseer ciertos atributos, que consisten en información adicional sobre el objeto. Uno de ellos es el atributo names, que permite que cada elemento dentro de un vector o una lista pueda tener su propio nombre, así como también que cada fila o columna de una matriz tenga su propio nombre, independientemente del identificador general del objeto.

Vectores

A cada elemento de un vector se le puede, opcionalmente, asignar un nombre. Esto se realiza de alguna de estas formas:

Opción 1: después de crear el vector

# El vector se llama "frutas" y tiene 4 elementos
frutas <- c(3, 7, 2, 1)
frutas

[1] 3 7 2 1

# Cada uno de estos elementos no tienen nombres
names(frutas)

NULL

# Le doy un nombre a cada elemento
names(frutas) <- c("manzanas", "naranjas", "bananas", "peras")
frutas

manzanas naranjas  bananas    peras 
       3        7        2        1

Opción 2: en el momento de crear el vector

frutas <- c(manzanas = 3, naranjas = 7, bananas = 2, peras = 1)
frutas

manzanas naranjas  bananas    peras 
       3        7        2        1

Los nombres son útiles porque permiten indexar al vector, sin necesidad de usar como índice la posición del elemento:

frutas[2]

naranjas 
       7

frutas["naranjas"]

naranjas 
       7

No todos los elementos de un vector deben tener nombre:

frutas <- c(manzanas = 3, 7, bananas = 2, 1)
frutas

manzanas           bananas          
       3        7        2        1

names(frutas)

[1] "manzanas" ""         "bananas"  ""

Matrices

En el caso de las matrices, se le puede asignar nombres a sus filas y columnas:

Opción 1: después de crear la matriz

x <- matrix(c( 8, 13, 18, 23, 
              11, 16, 21, 26, 
              14, 19, 24, 29), 
              nrow = 3, byrow = TRUE)
rownames(x) <- c("A", "B", "C")
colnames(x) <- c("grupo1", "grupo2", "grupo3", "grupo4")
x

  grupo1 grupo2 grupo3 grupo4
A      8     13     18     23
B     11     16     21     26
C     14     19     24     29

Opción 2: al crear la matriz

x <- matrix(c( 8, 13, 18, 23, 
              11, 16, 21, 26, 
              14, 19, 24, 29), 
            nrow = 3, byrow = TRUE,
            dimnames = list(Categorias = c("A", "B", "C"), 
                            Grupos = c("grupo1", "grupo2", "grupo3", "grupo4")))
x

          Grupos
Categorias grupo1 grupo2 grupo3 grupo4
         A      8     13     18     23
         B     11     16     21     26
         C     14     19     24     29

En este último ejemplo, se han elegido arbitrariamente los nombres Categorias y Grupos para llamar al conjunto completo de las filas y de las columnas, respectivamente. Esos nombres pueden ser cambiados por otros. Además, los nombres fueron encerrados en una lista, una estructura de datos que estudiaremos en breve.

Al igual que con los vectores, podemos usar los nombres de filas y columnas para indexar:

x["B", "grupo2"]

[1] 16

5.2.2 Operaciones vectorizadas

Con los conocimientos compartidos hasta aquí en esta unidad seremos capaces de escribir interesantes algoritmos para operar con vectores y matrices (por ejemplo: ordenar, buscar el mínimo, realizar cálculos algebraicos, etc.) y también de programarlos en R. En este proceso de aprendizaje, en la práctica de esta unidad vamos a encarar la tarea de escribir muchas funciones que, por lo general, ya forman parte de la sintaxis básica de cualquier lenguaje de programación. Sí… trabajaremos de más, ¡pero es para poder aprender! No obstante, ahora vamos a mencionar algunos ejemplos de funciones que ya están disponibles en R y que evitan que tengamos que trabajar tanto.

La mayoría de las funciones de R están vectorizadas. Esto quiere decir que están diseñadas para operar al mismo tiempo con todos los elementos de los vectores y matrices y no es necesario recorrer cada posición, una por una, como aprendimos para incorporar nuestros primeros conocimientos sobre algoritmos. Las funciones operan en todos los elementos sin tener que usar estructuras iterativas, haciendo que el código sea más conciso, fácil de leer y con menos chances de cometer errores.

Vectores

Por ejemplo, supongamos que queremos sumar dos vectores, como en el *ejercicio 2 de la práctica 4. Gracias a que la suma en R está vectorizada, esto se logra haciendo sencillamente:

u <- c(5, 8, 2)
v <- c(2, 3, -1)
suma <- u + v
suma

[1]  7 11  1

Sin vectorización, deberíamos diseñar y programar un algoritmo como el siguiente:

suma <- numeric(length(u))
for (i in 1:length(u)) { 
    suma[i] <- u[i] + v[i]
}
suma

[1]  7 11  1

Como podemos notar, al ejecutar u + v R realiza la suma elemento a elemento entre los dos vectores. Esto también sucede con los otros operadores aritméticos:

u - v

[1] 3 5 3

u * v

[1] 10 24 -2

u / v

[1]  2.500000  2.666667 -2.000000

u %% v

[1] 1 2 0

Estas operaciones también funcionan con vectores de distinto largo. En este caso, R aplica la regla del reciclaje: el vector más corto se recicla (se repiten sus elementos) hasta alcanzar la longitud del más largo y luego se opera elemento a elemento. Como es raro que queramos operar con dos vectores de distinto largo, R por las dudas nos tira una advertencia:

z <- c(1, 2)
u + z

Warning in u + z: longer object length is not a multiple of shorter object
length

[1]  6 10  3

Si hacemos operaciones que involucran a una constante y a un vector, R repetirá tal operación con cada elemento del vector:

u + 5

[1] 10 13  7

1 / v

[1]  0.5000000  0.3333333 -1.0000000

10 * z

[1] 10 20

(u + v) / 100

[1] 0.07 0.11 0.01

Si le aplicamos funciones matemáticas como log() o sqrt() a un vector, obtendremos como resultado el valor de dicha función en cada uno de los elementos del vector:

log(u)

[1] 1.6094379 2.0794415 0.6931472

sqrt(z)

[1] 1.000000 1.414214

Hay funciones que cuando se aplican a un vector, logran resumirlo siguiendo algún criterio:

Sumar todos los elementos de un vector:
```
sum(u)
```
```
[1] 15
```
Multiplicar todos los elementos de un vector:
```
prod(u)
```
```
[1] 80
```
Calcular el promedio de los elementos de un vector:
```
mean(u)
```
```
[1] 5
```

Encontrar el valor mínimo y su ubicación en el vector (como en el ejercicio 4 de la práctica 4):

x <- c(40, 70, 20, 90, 20)
min(x)

[1] 20

which.min(x) # si el mínimo se repite, esta es la posición del primero

[1] 3

which(x == min(x)) # si el mínimo se repite, esto muestra todas sus posiciones

[1] 3 5

Encontrar el valor máximo y su ubicación en el vector:

max(x)

[1] 90

which.max(x) # si el mínimo se repite, esta es la posición del primero

[1] 4

which(x == max(x)) # si el mínimo se repite, esto muestra todas sus posiciones

[1] 4

Combinando las ideas anteriores, podemos resolver de forma muy rápida ciertos problemas, como el de calcular el producto escalar entre dos vectores (ejercicio 5 de la práctica 4):

[1] 5 8 2

[1]  2  3 -1

sum(u * v)

[1] 32

En lo anterior, u * v hace la multiplicación elemento a elemento entre los vectores u y v y luego sumamos esos valores con sum(). Sin las operaciones vectorizadas, deberíamos hacer algo como lo siguiente:

rtdo <- 0
for (i in 1:length(u)) { 
    rtdo <- rtdo + u[i] * v[i]
}
rtdo

[1] 32

En el ejercicio 3 de la Práctica 4 creamos las funciones ordenar_asc() y ordenar_des() para ordenar los elementos de un vector. Con las funciones disponibles en R, esto se puede hacer así:

[1] 40 70 20 90 20

sort(x)

[1] 20 20 40 70 90

sort(x, decreasing = TRUE)

[1] 90 70 40 20 20

Matrices

Los casos anteriores tienen sus equivalentes cuando operamos con matrices. Por ejemplo, en el ejercicio 7 de la práctica 4 programamos una función para hacer la suma entre dos matrices. Sin vectorización, esto involucra pasos como los siguientes:

a <- matrix(c(5, 8, 2, 2, 3, 1), nrow = 3)
b <- matrix(c(0, -1, 3, 1, 2, 4), nrow = 3)
a

     [,1] [,2]
[1,]    5    2
[2,]    8    3
[3,]    2    1

     [,1] [,2]
[1,]    0    1
[2,]   -1    2
[3,]    3    4

suma <- matrix(NA, nrow(a), ncol(a))
for (i in 1:nrow(a)) {
    for (j in 1:ncol(a)) {
        suma[i, j] <- a[i, j] + b[i, j]
    }
}
suma

     [,1] [,2]
[1,]    5    3
[2,]    7    5
[3,]    5    5

Gracias a las operaciones vectorizadas de R, esto se puede resumir en:

a + b

     [,1] [,2]
[1,]    5    3
[2,]    7    5
[3,]    5    5

A continuación, otros ejemplos de operaciones realizadas elemento a elemento con matrices:

a + b

     [,1] [,2]
[1,]    5    3
[2,]    7    5
[3,]    5    5

a - b

     [,1] [,2]
[1,]    5    1
[2,]    9    1
[3,]   -1   -3

a * b

     [,1] [,2]
[1,]    0    2
[2,]   -8    6
[3,]    6    4

a / b

           [,1] [,2]
[1,]        Inf 2.00
[2,] -8.0000000 1.50
[3,]  0.6666667 0.25

a^2

     [,1] [,2]
[1,]   25    4
[2,]   64    9
[3,]    4    1

sqrt(a)

         [,1]     [,2]
[1,] 2.236068 1.414214
[2,] 2.828427 1.732051
[3,] 1.414214 1.000000

También podemos resumir la información contenida en una matriz:

Suma de todos los elementos:

     [,1] [,2]
[1,]    5    2
[2,]    8    3
[3,]    2    1

sum(a)

[1] 21

Promedio de todos los elementos:
```
mean(a)
```
```
[1] 3.5
```
Suma de los elementos por fila:
```
rowSums(a)
```
```
[1]  7 11  3
```
Suma de los elementos por columna:
```
colSums(a)
```
```
[1] 15  6
```
Promedio de los elementos por fila:
```
rowMeans(a)
```
```
[1] 3.5 5.5 1.5
```
Promedio de los elementos por columna:
```
colMeans(a)
```
```
[1] 5 2
```

Búsqueda de mínimos y máximos en una matriz:

d <- matrix(sample(100, 20), nrow = 5)

# Valor máximo
max(d)

[1] 99

# Posición (arr.ind = TRUE para que nos indique fila y columna)
which(d == max(d), arr.ind = TRUE)

     row col
[1,]   4   4

# Valor mínimo
min(d)

[1] 8

# Posición
which(d == min(d), arr.ind = TRUE)

     row col
[1,]   2   1

Como aprenderán en Álgebra, las matrices numéricas son muy útiles en diversos campos y por eso existen distintas operaciones que se pueden realizar con las mismas. Veamos algunos ejemplos de la aplicación del álgebra matricial en R:

Transpuesta de una matriz:

     [,1] [,2]
[1,]    5    2
[2,]    8    3
[3,]    2    1

t(a)

     [,1] [,2] [,3]
[1,]    5    8    2
[2,]    2    3    1

Producto entre dos matrices:

e <- matrix(1:4, nrow = 2)
a

     [,1] [,2]
[1,]    5    2
[2,]    8    3
[3,]    2    1

     [,1] [,2]
[1,]    1    3
[2,]    2    4

a %*% e

     [,1] [,2]
[1,]    9   23
[2,]   14   36
[3,]    4   10

Inversa de la matriz:

solve(e)

     [,1] [,2]
[1,]   -2  1.5
[2,]    1 -0.5

Obtener los elementos de la diagonal principal:
```
diag(d)
```
```
[1] 33 23 52 99
```

5.2.3 Operaciones lógicas vectorizadas

Cuando dos vectores o matrices se vinculan a través de una comparación, se opera elemento a elemento obteniendo un vector o matriz de valores lógicos:

x <- c(40, 70, 20, 90, 20)
y <- c(10, 70, 30, 15, 21)
x > y

[1]  TRUE FALSE FALSE  TRUE FALSE

x < y * 5

[1]  TRUE  TRUE  TRUE FALSE  TRUE

a <- matrix(c(5, 8, 2, 2, 3, 1), nrow = 3)
b <- matrix(c(0, -1, 3, 1, 2, 4), nrow = 3)
a

     [,1] [,2]
[1,]    5    2
[2,]    8    3
[3,]    2    1

     [,1] [,2]
[1,]    0    1
[2,]   -1    2
[3,]    3    4

a != b

     [,1] [,2]
[1,] TRUE TRUE
[2,] TRUE TRUE
[3,] TRUE TRUE

a > b

      [,1]  [,2]
[1,]  TRUE  TRUE
[2,]  TRUE  TRUE
[3,] FALSE FALSE

Si un vector o matriz de valores lógicos y queremos saber si todos o al menos uno de los elementos es igual a TRUE, podemos usar las funciones all() y any(), respectivamente:

all(a != b)

[1] TRUE

any(a != b)

[1] TRUE

all(a > b)

[1] FALSE

any(a > b)

[1] TRUE

Las operaciones de comparación pueden hacerse entre cada elemento de un vector o matriz y un único valor:

x < 50

[1]  TRUE FALSE  TRUE FALSE  TRUE

a == 3

      [,1]  [,2]
[1,] FALSE FALSE
[2,] FALSE  TRUE
[3,] FALSE FALSE

b > 0

      [,1] [,2]
[1,] FALSE TRUE
[2,] FALSE TRUE
[3,]  TRUE TRUE

Los operadores lógicos que se utilizan para realizar cálculos elemento a elemento con vectores y matrices son &, \ y !. Ellos nos permiten crear expresiones aún más complejas:

x < 50 & y > 50

[1] FALSE FALSE FALSE FALSE FALSE

a < 0 | b > 0

      [,1] [,2]
[1,] FALSE TRUE
[2,] FALSE TRUE
[3,]  TRUE TRUE

!(x <= 50)

[1] FALSE  TRUE FALSE  TRUE FALSE

5.2.4 Uso de vectores para indexar vectores y matrices

Como ya sabemos, indexar es hacer referencia a uno o más elementos particulares dentro de una estructura de datos. Vimos que para indexar a un vector, hace falta sólo un índice:

x <- c(10.4, 5.6, 3.1, 6.4, 21.7)
x[3]

[1] 3.1

Y que para indexar matrices, son necesarios dos índices:

a <- matrix(c(4,-2, 1, 20, -7, 12, -8, 13, 17), nrow = 3)
a

     [,1] [,2] [,3]
[1,]    4   20   -8
[2,]   -2   -7   13
[3,]    1   12   17

a[2, 3]

[1] 13

Pero también podemos indexar a múltiples elementos de un vector o una matriz a la vez:

Vectores

# Mostrar los primeros tres elementos del vector x
x[1:3]

[1] 10.4  5.6  3.1

# Mostrar los elementos en las posiciones 2 y 4
x[c(2, 4)]

[1] 5.6 6.4

# Mostrar el último elemento
x[length(x)]

[1] 21.7

# Indexar con valores lógicos. Obtenemos sólo las posiciones indicadas con TRUE:
x[c(F, F, T, T, F)]

[1] 3.1 6.4

# Sabiendo que la siguiente operación devuelve TRUE o FALSE para cada posición de x:
x > 10

[1]  TRUE FALSE FALSE FALSE  TRUE

# ...la podemos usar para quedarnos con aquellos elementos de x mayores a 10:
x[x > 10]

[1] 10.4 21.7

#Mostrar todos los elementos menos el cuarto
x[-4]

[1] 10.4  5.6  3.1 21.7

Matrices

# Toda la fila 3
a[3, ]

[1]  1 12 17

# Toda la columna 2
a[, 2]

[1] 20 -7 12

# Submatriz con las columnas 1 y 2
a[, 1:2]

     [,1] [,2]
[1,]    4   20
[2,]   -2   -7
[3,]    1   12

# Submatriz con las columnas 1 y 3
a[, c(1, 3)]

     [,1] [,2]
[1,]    4   -8
[2,]   -2   13
[3,]    1   17

# Asignar el mismo valor en toda la fila 3
a[3, ] <- 10
a

     [,1] [,2] [,3]
[1,]    4   20   -8
[2,]   -2   -7   13
[3,]   10   10   10

5.2.5 La función `apply()`

Supongamos que queremos encontrar el máximo valor en cada fila de una matriz. Podemos lograrlo de la siguiente forma. Creamos un vector maximos con lugar para guardar el máximo de cada fila. Luego, iteramos para recorrer cada fila de la matriz, buscar el mínimo y guardarlo en el vector maximos:

     [,1] [,2] [,3]
[1,]    4   20   -8
[2,]   -2   -7   13
[3,]   10   10   10

maximos <- numeric(nrow(a))
for (i in 1:nrow(a)) {
    maximos[i] <- max(a[i, ])
}
maximos

[1] 20 13 10

En R existe una forma más práctica y eficiente de conseguir el mismo resultado:

apply(a, 1, max)

[1] 20 13 10

La función apply() sirve para aplicar una misma operación a cada fila o columna de una matriz. En el ejemplo anterior:

el primer argumento, a, es la matriz a analizar.
el segundo argumento, 1, indica que la operación se realizará fila por fila (para que se haga por columna, debemos indicar 2)
el tercer argumento, max, es el nombre de la función que se le aplica a cada fila.

De manera similar, podemos encontrar el mínimo valor de cada columna:

apply(a, 2, min)

[1] -2 -7 -8

5.2.6 Generación de vectores con secuencias numéricas

A continuación mostramos cómo generar algunos vectores numéricos en R:

# Enteros de 1 a 5
1:5

[1] 1 2 3 4 5

# Números de 1 a 10 cada 2
seq(1, 10, 2)

[1] 1 3 5 7 9

# Números de 0 a -1 cada -0.1
seq(0, -1, -0.1)

 [1]  0.0 -0.1 -0.2 -0.3 -0.4 -0.5 -0.6 -0.7 -0.8 -0.9 -1.0

# Siete números equiespaciados entre 0 y 1
seq(0, 1, length.out = 7)

[1] 0.0000000 0.1666667 0.3333333 0.5000000 0.6666667 0.8333333 1.0000000

# Repetir el 1 tres veces
rep(1, 3)

[1] 1 1 1

# Repetir (1, 2, 3) tres veces
rep(1:3, 3)

[1] 1 2 3 1 2 3 1 2 3

# Repetir cada número tres veces
rep(1:3, each = 3)

[1] 1 1 1 2 2 2 3 3 3

# Generar una matriz diagonal
diag(c(3, 7, 1, 5))

     [,1] [,2] [,3] [,4]
[1,]    3    0    0    0
[2,]    0    7    0    0
[3,]    0    0    1    0
[4,]    0    0    0    5

# Generar una matriz identidad
diag(rep(1, 5))

     [,1] [,2] [,3] [,4] [,5]
[1,]    1    0    0    0    0
[2,]    0    1    0    0    0
[3,]    0    0    1    0    0
[4,]    0    0    0    1    0
[5,]    0    0    0    0    1

5.2.7 Concatenación de vectores y matrices

Los vectores pueden combinarse entre sí para crear nuevos vectores con c():

x <- 1:5
y <- c(10, 90, 87)
z <- c(x, y, x)
z

 [1]  1  2  3  4  5 10 90 87  1  2  3  4  5

Matrices que tienen la misma cantidad de filas pueden concatenarse una al lado de la otra con cbind():

a <- matrix(c(5, 8, 2, 2, 3, 1), nrow = 3)
b <- matrix(c(0, -1, 3, 1, 2, 4), nrow = 3)
a

     [,1] [,2]
[1,]    5    2
[2,]    8    3
[3,]    2    1

     [,1] [,2]
[1,]    0    1
[2,]   -1    2
[3,]    3    4

d <- cbind(a, b)
d

     [,1] [,2] [,3] [,4]
[1,]    5    2    0    1
[2,]    8    3   -1    2
[3,]    2    1    3    4

Matrices que tienen la misma cantidad de columnas pueden concatenarse una debajo de la otra con cbind():

e <- rbind(a, b)
e

     [,1] [,2]
[1,]    5    2
[2,]    8    3
[3,]    2    1
[4,]    0    1
[5,]   -1    2
[6,]    3    4

Estas funciones también permiten unir matrices con vectores:

x <- 1:6
cbind(e, x)

          x
[1,]  5 2 1
[2,]  8 3 2
[3,]  2 1 3
[4,]  0 1 4
[5,] -1 2 5
[6,]  3 4 6

5.2.8 Listas

Una de las principales características de los arreglos es la homegeneidad: todos los elementos que contienen deben ser del mismo tipo. No se puede, por ejemplo, mezclar en una matriz valores numéricos y lógicos. Sin embargo, en muchos problemas resulta útil contar con alguna estructura de datos que permita agrupar objetos de diversos tipos. Esa es, justamente, la definición de una lista. Podemos imaginarla como una bolsa en la cual podemos meter todo tipo de objetos, incluyendo vectores, matrices y, por qué no, otras bolsas (es decir, bolsas dentro de una bolsa o listas dentro de una lista). Todos los lenguajes de programación proveen algún tipo de estructura con estas características, aunque no todos las llaman igual. Otros posibles nombres con los que se conocen pueden ser tupla o agregado. En R se llaman listas o vectores recursivos. El siguiente diagrama presenta una lista (recuadro con puntas redondeadas) que contiene:

Un vector numérico de largo 3.
Un vector carácter de largo 2.
Una matriz numérica de dimensión 2x2.
Un valor lógico.

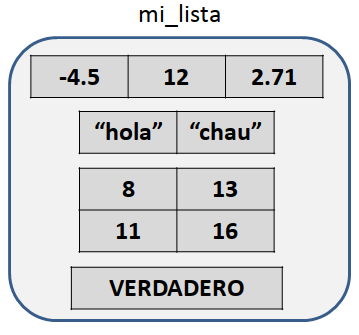
Figura 5.13: Ejemplo de una lista

La creación de esta lista se realiza mediante la función list(), cuyos argumentos son los elementos que queremos guardar en la lista, separados por comas:

mi_lista <- list(
    c(-4.5, 12, 2.71),
    c("hola", "chau"),
    matrix(c(8, 11, 13, 16), nrow = 2),
    TRUE
)
mi_lista

[[1]]
[1] -4.50 12.00  2.71

[[2]]
[1] "hola" "chau"

[[3]]
     [,1] [,2]
[1,]    8   13
[2,]   11   16

[[4]]
[1] TRUE

Luego de correr la sentencia anterior, podemos ver que mi_lista es un nuevo objeto disponible en el ambiente global y como tal está listado en el panel Environment. Allí se nos indica que se trata de una lista y, además, podemos previsualizar su contenido al hacer clic en el círculo celeste que antecede a su nombre:

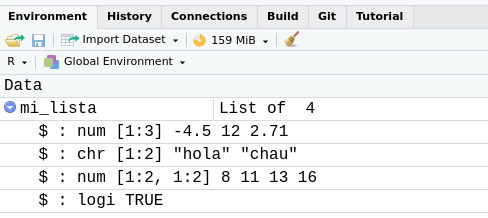
Figura 5.14: La lista en la pestaña Environment de RStudio

Usamos dobles corchetes [[ ]] para referenciar a cada objeto que forma parte de la lista. Además, si queremos indicar un elemento dentro de un objeto que forma parte de la lista, agregamos otro conjunto de corchetes como hacemos con vectores y matrices. Por ejemplo:

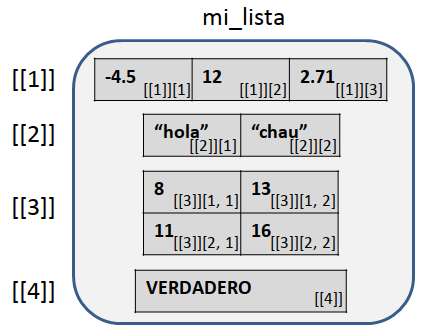
Figura 5.15: Ejemplo de una lista

mi_lista[[1]]

[1] -4.50 12.00  2.71

mi_lista[[1]][3]

[1] 2.71

mi_lista[[2]]

[1] "hola" "chau"

mi_lista[[2]][2]

[1] "chau"

mi_lista[[3]]

     [,1] [,2]
[1,]    8   13
[2,]   11   16

mi_lista[[3]][2, 1]

[1] 11

mi_lista[[4]]

[1] TRUE

mi_lista[[4]][1]

[1] TRUE

Podemos asignar valor a algún elemento usando los índices de esa misma forma:

mi_lista[[1]][3] <- 0
mi_lista

[[1]]
[1] -4.5 12.0  0.0

[[2]]
[1] "hola" "chau"

[[3]]
     [,1] [,2]
[1,]    8   13
[2,]   11   16

[[4]]
[1] TRUE

Cada uno de los elementos de una lista puede tener un nombre propio. Podemos asignarle un nombre a uno, algunos o todos los integrantes en una lista:

mi_lista <- list(
    w = c(-4.5, 12, 2.71),
    x = c("hola", "chau"),
    y = matrix(c(8, 11, 13, 16), nrow = 2),
    z = TRUE
)
mi_lista

$w
[1] -4.50 12.00  2.71

$x
[1] "hola" "chau"

$y
     [,1] [,2]
[1,]    8   13
[2,]   11   16

$z
[1] TRUE

Esto amplía las opciones para hacer referencia a cada objeto y elemento allí contenido. Las siguientes sentencias son todas equivalentes y sirven para acceder al tercer elemento de la lista, cuyo nombre es y:

mi_lista[[3]]

     [,1] [,2]
[1,]    8   13
[2,]   11   16

mi_lista[["y"]]

     [,1] [,2]
[1,]    8   13
[2,]   11   16

mi_lista$y

     [,1] [,2]
[1,]    8   13
[2,]   11   16

Finalmente, consideremos la situación en la cual queremos aplicarle la misma función a cada uno de los elementos que integran una lista. Para esto podemos usar lapply() o sapply(), parientes de la función apply() que vimos antes. Por ejemplo, tenemos una lista con varios vectores y queremos saber el largo de cada uno de ellos:

mi_lista <- list(x = c(1, 8, 9, -1), y = c("uno", "dos", "tres"), z = c(3, 2))
mi_lista

$x
[1]  1  8  9 -1

$y
[1] "uno"  "dos"  "tres"

$z
[1] 3 2

Podemos ver el largo de cada elemento de la lista, uno por uno:

length(mi_lista$x)

[1] 4

length(mi_lista$y)

[1] 3

length(mi_lista$z)

[1] 2

O podemos hacerlo así:

lapply(mi_lista, length)

$x
[1] 4

$y
[1] 3

$z
[1] 2

sapply(mi_lista, length)

x y z 
4 3 2

Ambas funciones le aplican la función elegida como segundo argumento (length()) a cada elemento de la lista indicada en el primer argumento (mi_lista). La diferencia entre ellas es que lapply() devuelve una nueva lista con los resultados, mientras que sapply() los devuelve acomodados en un vector²³.

Ejemplo: función que devuelve una lista

En el capítulo anterior, dijimos que las funciones son subalgoritmos que podían devolver exactamente un objeto como resultado. Esto puede ser una limitación, ya que en algunos casos tal vez necesitemos devolver varios elementos de distinto tipo ²⁴ . La solución consiste en devolver una lista que englobe a todos los objetos que nos interese que la función le entregue como resultado al algoritmo principal que la invocó. Como una lista es un único objeto, ¡la función puede devolverla sin ningún problema!

Para ejemplificar, recordemos el siguiente ejercicio de la práctica 3: escribir un programa para la creación de la función triangulos(a, b, c) que a partir de la longitud de los tres lados de un triángulo a, b y d (valores positivos) lo clasifica con los siguientes resultados posibles: no forman un triángulo (un lado mayor que la suma de los otros dos), triángulo equilátero, isósceles o escaleno. Vamos a modificar la función para que tenga el siguiente comportamiento: la función debe devolver el tipo de triángulo como cadena de texto y el valor numérico del perímetro del mismo (o un 0 si no es triángulo). Es decir, la función debe devolver tanto un objeto de tipo carácter y otro de tipo numérico. Para lograrlo los encerraremos en una lista:

#-----------------------------------------------------
# Función triangulos
# Clasifica un triángulo según la longitud de sus lados
# Entrada:
#       - a, b, d, números reales positivos
# Salida:
#       - una lista cuyo primer elemento es un carácter que indica el tipo de
#       triángulo y cuyo segundo elemento es el perímetro del triángulo o el valor 0
#       si los lados provistos no corresponden a un triángulo
#-----------------------------------------------------
triangulos <- function(a, b, d) {
    perimetro <- a + b + d
    if (a > b + d || b > a + d || d > a + b) {
        tipo <- "no es triángulo"
        perimetro <- 0
    } else if (a == b & a == d) {
        tipo <- "equilátero"
    } else if (a == b || a == d || b == d) {
        tipo <- "isósceles"
    } else {
        tipo <- "escaleno"
    }
    return(list(tipo = tipo, perimetro = perimetro))
    # atención con tipo = tipo: la primera vez es el nombre que le estamos dando
    # al elemento de la lista, la segunda vez es la variable que guardamos en la lista
}

Ejemplos del uso de esta función:

# Guardamos el resultado devuelto (una lista) en el objeto resultado
resultado <- triangulos(2, 3, 4)
# Miramos el primer elemento de la lista (carácter que indica el tipo)
resultado[[1]]

[1] "escaleno"

resultado$tipo

[1] "escaleno"

# Miramos el primer elemento de la lista (perímetro)
resultado[[2]]

[1] 9

resultado$perimetro

[1] 9

# Miramos todo junto
resultado

$tipo
[1] "escaleno"

$perimetro
[1] 9

# Otro ejemplo:
resultado2 <- triangulos(2, 3, 10)
resultado2[[1]]

[1] "no es triángulo"

resultado2[[2]]

[1] 0

5.3 Otras consideraciones (lectura opcional)

Dependiendo de cómo se almacenan los datos que componen a una estructura en el hardware de la computadora, las mismas se pueden clasificar en contiguas o enlazadas. En las estructuras contiguas, los datos se sitúan en áreas adyacentes de memoria y cada uno de ellos se puede localizar partiendo de la posición en memoria del primer elemento de la estructura. En las estructuras enlazadas, los datos no se sitúan necesariamente de forma continua en la memoria sino que existen punteros (otro tipo de dato que apunta hacia determinada posición de memoria) que permite identificar cuál es el orden de los elementos dentro de la estructura.

Por otro lado, las estructuras también se pueden clasificar en dinámicas o estáticas, según si su tamaño puede cambiar o no durante la ejecución de un programa, respectivamente. Cuando se emplea una estructura estática, se declara con anterioridad el tamaño que ocupará en memoria y su dimensión no podrá variar, aún cuando no se ocupen todas las posiciones reservadas. En contraposición, una estructura dinámica puede cambiar en tamaño.

Antes se mencionó que las listas de R pueden contener objetos de distintos tipos. Para ser más rigurosos, una lista es un tipo especial de vector que agrupa punteros hacia distintos objetos. Técnicamente, todos los elementos de una lista son del mismo tipo (punteros), pero hacen referencia a distintos objetos, dándonos la impresión de que en una lista de R, sencillamente, podemos meter cualquier tipo de objeto.

5.4 Arreglos multidimensionales (lectura opcional)

Un arreglo multidimensional contiene más de dos dimensiones, es decir, requiere más de dos índices para identificar a cada uno de sus elementos. La representación matemática o visual ya no es tan sencilla como la de los vectores o matrices. Para interpretarlos o saber cuándo usarlos, pensamos que cada una de las dimensiones representa una característica de los elementos.

Por ejemplo, imaginemos que en un local comercial se quiere registrar cuántos clientes se atendieron en cada una de las tres cajas disponibles (primer dimensión del arreglo: caja 1, caja 2 o caja 3), ya sea en el turno mañana o tarde (segunda dimensión: 1 para la mañana o 2 para la tarde) en cada día hábil de una semana (tercera dimensión: 1 lunes, 2 martes, 3 miércoles, 4 jueves o 5 viernes). Si queremos registrar, por ejemplo, que la caja 1 en el turno tarde del día jueves atendió 12 clientes, tenemos que guardar el valor 12 en la posición [1, 2, 4] del arreglo.

El arreglo de 3 dimensiones que permite acomodar toda la información del ejemplo en una sola estructura puede definirse en R así:

clientes <- array(0, dim = c(3, 2, 5))
clientes

, , 1

     [,1] [,2]
[1,]    0    0
[2,]    0    0
[3,]    0    0

, , 2

     [,1] [,2]
[1,]    0    0
[2,]    0    0
[3,]    0    0

, , 3

     [,1] [,2]
[1,]    0    0
[2,]    0    0
[3,]    0    0

, , 4

     [,1] [,2]
[1,]    0    0
[2,]    0    0
[3,]    0    0

, , 5

     [,1] [,2]
[1,]    0    0
[2,]    0    0
[3,]    0    0

Luego, si queremos registrar que la caja 1 en el turno tarde del día jueves atendió 12 clientes, hacemos:

clientes[1, 2, 4] <- 12
clientes

, , 1

     [,1] [,2]
[1,]    0    0
[2,]    0    0
[3,]    0    0

, , 2

     [,1] [,2]
[1,]    0    0
[2,]    0    0
[3,]    0    0

, , 3

     [,1] [,2]
[1,]    0    0
[2,]    0    0
[3,]    0    0

, , 4

     [,1] [,2]
[1,]    0   12
[2,]    0    0
[3,]    0    0

, , 5

     [,1] [,2]
[1,]    0    0
[2,]    0    0
[3,]    0    0

En R, podemos ponerle un nombre a cada una de las dimensiones del arreglo (“caja”, “turno”, “dia”), para poder identificar mejor a qué aspecto hace referencia y, a su vez, un nombre a cada una de sus modalidades (por ejemplo, “caja 1”, “caja 2” o “caja 3”). Esto se logra de la siguiente forma:

dimnames(clientes) <- list(caja = c("caja 1", "caja 2", "caja 3"),
                           turno = c("mañana", "tarde"),
                           dia = c("lun", "mar", "mie", "jue", "vie"))
clientes

, , dia = lun

        turno
caja     mañana tarde
  caja 1      0     0
  caja 2      0     0
  caja 3      0     0

, , dia = mar

        turno
caja     mañana tarde
  caja 1      0     0
  caja 2      0     0
  caja 3      0     0

, , dia = mie

        turno
caja     mañana tarde
  caja 1      0     0
  caja 2      0     0
  caja 3      0     0

, , dia = jue

        turno
caja     mañana tarde
  caja 1      0    12
  caja 2      0     0
  caja 3      0     0

, , dia = vie

        turno
caja     mañana tarde
  caja 1      0     0
  caja 2      0     0
  caja 3      0     0

Para situaciones como la anterior, resulta más útil guardar los valores en otros tipos de estructuras especializadas en conjuntos de datos, como veremos más adelante. Por esta razón, en esta asignatura no profundizaremos en el estudio de arreglos multidimensionales y nos bastaremos con vectores y matrices. Sin embargo, debemos saber de su existencia porque son estructuras útiles para ciertas tareas de programación.

4 Descomposición algorítmica

6 Uso de archivos de datos

5 Estructuras de datos

5.1 Arreglos

5.1.1 Arreglos unidimensionales o vectores

5.1.2 Arreglos bidimensionales o matrices

5.2 Características particulares de las estructuras de datos en R

5.2.1 Elementos con nombre

5.2.2 Operaciones vectorizadas

5.2.3 Operaciones lógicas vectorizadas

5.2.4 Uso de vectores para indexar vectores y matrices

5.2.5 La función apply()

5.2.6 Generación de vectores con secuencias numéricas

5.2.7 Concatenación de vectores y matrices

5.2.8 Listas

5.3 Otras consideraciones (lectura opcional)

5.4 Arreglos multidimensionales (lectura opcional)

5.2.5 La función `apply()`