3  Resolución de sistemas de ecuaciones lineales

3.1 Introducción

• Objetivo de la unidad: examinar los aspectos numéricos que se presentan al resolver sistemas de ecuaciones lineales de la forma:

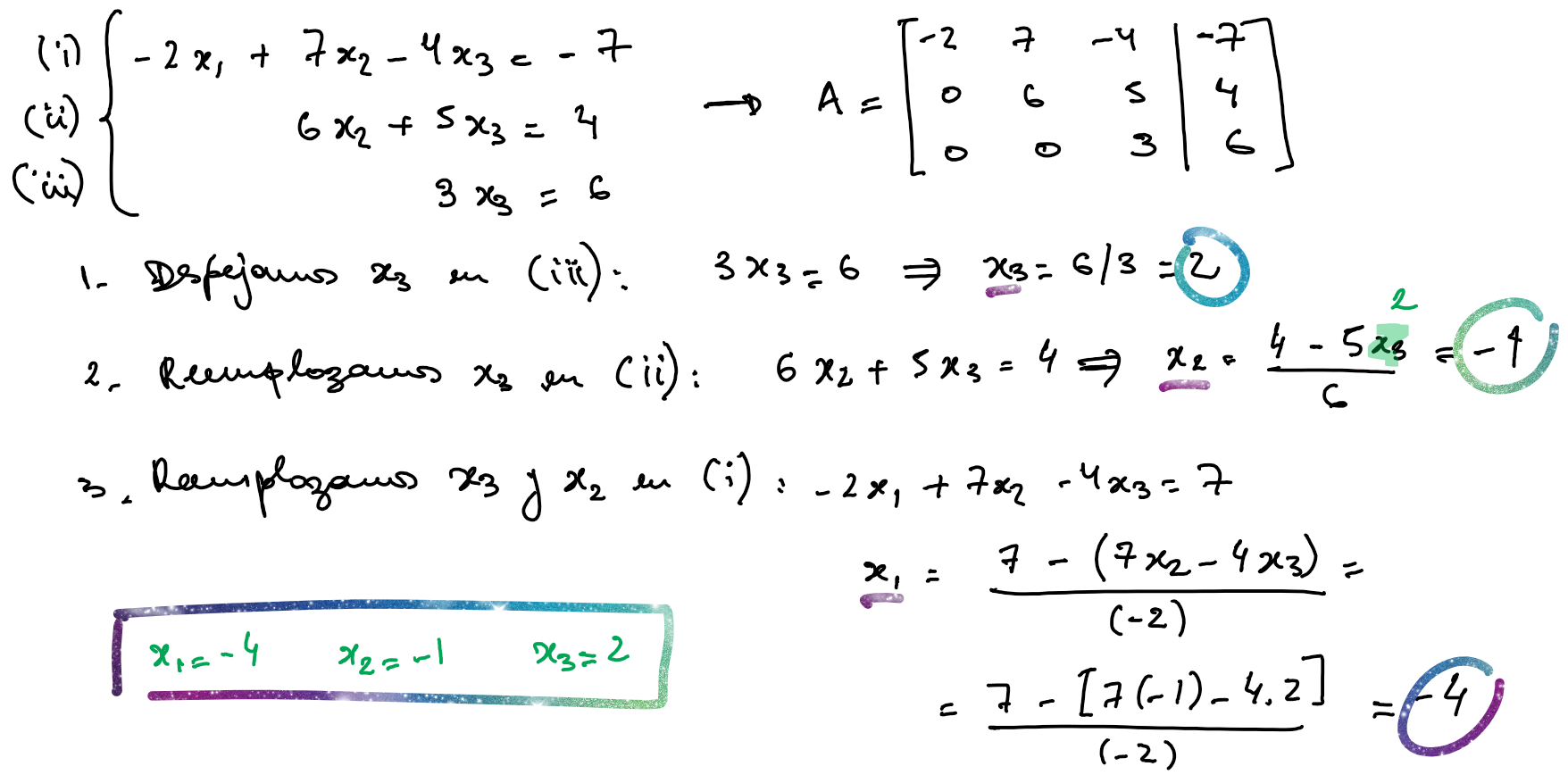
\[ \begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2 \\ \vdots \\ a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n = b_n \end{cases} \]

• El anterior es un sistema de \(n\) ecuaciones con \(n\) incógnitas: decimos que es un sistema de orden \(n \times n\), en el cual los coeficientes \(a_{ij}\) y los términos independientes \(b_i\) son reales fijos.
• Recordemos que los sistemas de ecuaciones lineales se puede representar matricialmente: \(\mathbf{Ax=b}\), de dimensión \(n\times n\), \(n\times 1\) y \(n\times 1\), respectivamente.

\[ \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix} \times \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix} \]

• Llamamos matriz ampliada o aumentada a:

\[ \begin{bmatrix} \mathbf{A}, & \mathbf{b} \end{bmatrix} = \begin{bmatrix} \begin{array}{cccc|c} a_{11} & a_{12} & \cdots & a_{1n} & b_1\\ a_{21} & a_{22} & \cdots & a_{2n} & b_2\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} & b_n \end{array} \end{bmatrix} \]

3.1.1 Repaso de lo que ya sabemos

• Un sistema de ecuaciones lineales se clasifica en:

  • Compatible determinado: tiene una única solución
  • Compatible indeterminado: tiene infinitas soluciones
  • Incompatible: no existe solución

• Además, las siguientes condiciones son equivalentes:

  • El sistema \(\mathbf{Ax=b}\) tiene solución única (es compatible determinado).
  • La matriz \(\mathbf{A}\) es invertible (existe \(\mathbf{A^{-1}}\)).
  • La matriz \(\mathbf{A}\) es no singular (\(\det \mathbf{A} \neq 0\)).
  • El sistema \(\mathbf{Ax=0}\) tiene como única solución \(\mathbf{x=0}\).

• Dos sistemas de orden \(n \times n\) son equivalentes si tienen el mismo conjunto de soluciones.

• Existen ciertas transformaciones sobre las ecuaciones de un sistema que no cambian el conjunto de soluciones (producen un sistema equivalente). Si llamamos con \(E_i\) a cada una de las ecuaciones del sistema:

  • Intercambio. El orden de las ecuaciones puede cambiarse: \(E_i \leftrightarrow E_j\)
  • Escalado. Multiplicar una ecuación por una constante no nula: \(\lambda E_i \rightarrow E_i\)
  • Sustitución: una ecuación puede ser reemplazada por una combinación lineal de las ecuaciones del sistema (teorema fundamental de la equivalencia). Por ejemplo: \(E_i + \lambda E_j \rightarrow E_i\)

• Mediante una secuencia de estas operaciones, un sistema lineal se transforma en uno nuevo más fácil de resolver y con las mismas soluciones.

• Realizar estas transformaciones sobre las ecuaciones es equivalente a realizar las mismas operaciones sobre las filas de la matriz aumentada.

3.1.2 Notación

• En esta sección presentamos la notación que utilizaremos para expresar algoritmos con operaciones matriciales (facilitando su programación).

• Dada una matriz \(\mathbf{Z}\) de dimensión \(n \times m\), anotamos:

  • \(z_{ij} = \mathbf{Z}[i, j]\): elemento en la fila \(i\) y columna \(j\) de la matriz \(\mathbf{Z}\)
  • \(\mathbf{Z}[i,]\): vector fila de dimensión \(1\times m\) constituido por la \(i\)-ésima fila de la matriz \(\mathbf{Z}\)
  • \(\mathbf{Z}[,j]\): vector columna \(n\times 1\) constituido por la \(j\)-ésima columna de la matriz \(\mathbf{Z}\)
  • \(\mathbf{Z}[i,k:l]\): matriz de dimensión \(1\times (l-k+1)\) constituida con los elementos \(z_{i,k}, z_{i,k+1}, \cdots, z_{i,l}\) de la matriz \(\mathbf{Z}\), \(l \geq k\).
  • \(\mathbf{Z}[c:d,k:l]\): matriz de dimensión \((d-c+1)\times (l-k+1)\) constituida por la submatriz que contiene las filas de \(\mathbf{Z}\) desde la \(c\) hasta \(d\) y las columnas de \(\mathbf{Z}\) desde la \(k\) hasta la \(l\), \(d \geq c\), \(l \geq k\).

• Dado un vector \(\mathbf{Z}\) de largo \(n\), anotamos:

  • \(\mathbf{Z}[i]\): elemento \(i\)-ésimo del vector \(\mathbf{Z}\)
  • \(\mathbf{Z}[k:l]\): vector de largo \((l-k+1)\) constituido con los elementos \(z_{k}, z_{k+1}, \cdots, z_{l}\) del vector \(\mathbf{Z}\), \(l \geq k\).

3.1.3 Métodos de resolución de sistemas de ecuaciones

• Métodos exactos: permiten obtener la solución del sistema de manera directa.

  • Método de sustitución hacia atrás o hacia adelante
  • Método de Eliminación de Gauss
  • Método de Gauss-Jordan

• Métodos aproximados: utilizan algoritmos iterativos que calculan las solución del sistema por aproximaciones sucesivas.

  • Método de Jacobi
  • Método de Gauss-Seidel

• En muchas ocasiones los métodos aproximados permiten obtener un grado de exactitud superior al que se puede obtener empleando los denominados métodos exactos, debido fundamentalmente a los errores de redondeo que se producen en el proceso.

3.2 Métodos exactos

• En esta sección repasaremos los métodos que ya conocen y que han aplicado “a mano” muchas veces para resolver sistemas de ecuaciones, con la particularidad de que pensaremos cómo expresar sus algoritmos para poder programarlos en la computadora.
• Entre los aspectos que tendremos que considerar, se encuentra la necesidad de aplicar estrategias de pivoteo (para evitar un pivote igual a cero cuando se resuelve el sistema) y la posibilidad de realizar reordenamientos de la matriz de coeficientes para disminuir los errores de redondeo producidos en los cálculos computacionales.

3.2.1 Sistemas con matriz de coeficientes diagonal

• Si la matriz de coeficientes es de esta forma:

  \[ \begin{bmatrix} a_{11} & 0 & \cdots & 0 \\ 0 & a_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_{nn} \end{bmatrix} \times \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix} \]

  el sistema se reduce a \(n\) ecuaciones simples y la solución sencillamente es:

  \[ \mathbf{x} = \begin{bmatrix} b_1/a_{11} \\ b_2/a_{22} \\ \vdots \\ b_n/a_{nn} \end{bmatrix} \]

3.2.2 Sistemas con matriz de coeficientes triangular

• Veamos el siguiente ejemplo y su resolución, que seguramente comprendemos sin problema:

knitr::include_graphics("Plots/U3/pizarra1.png")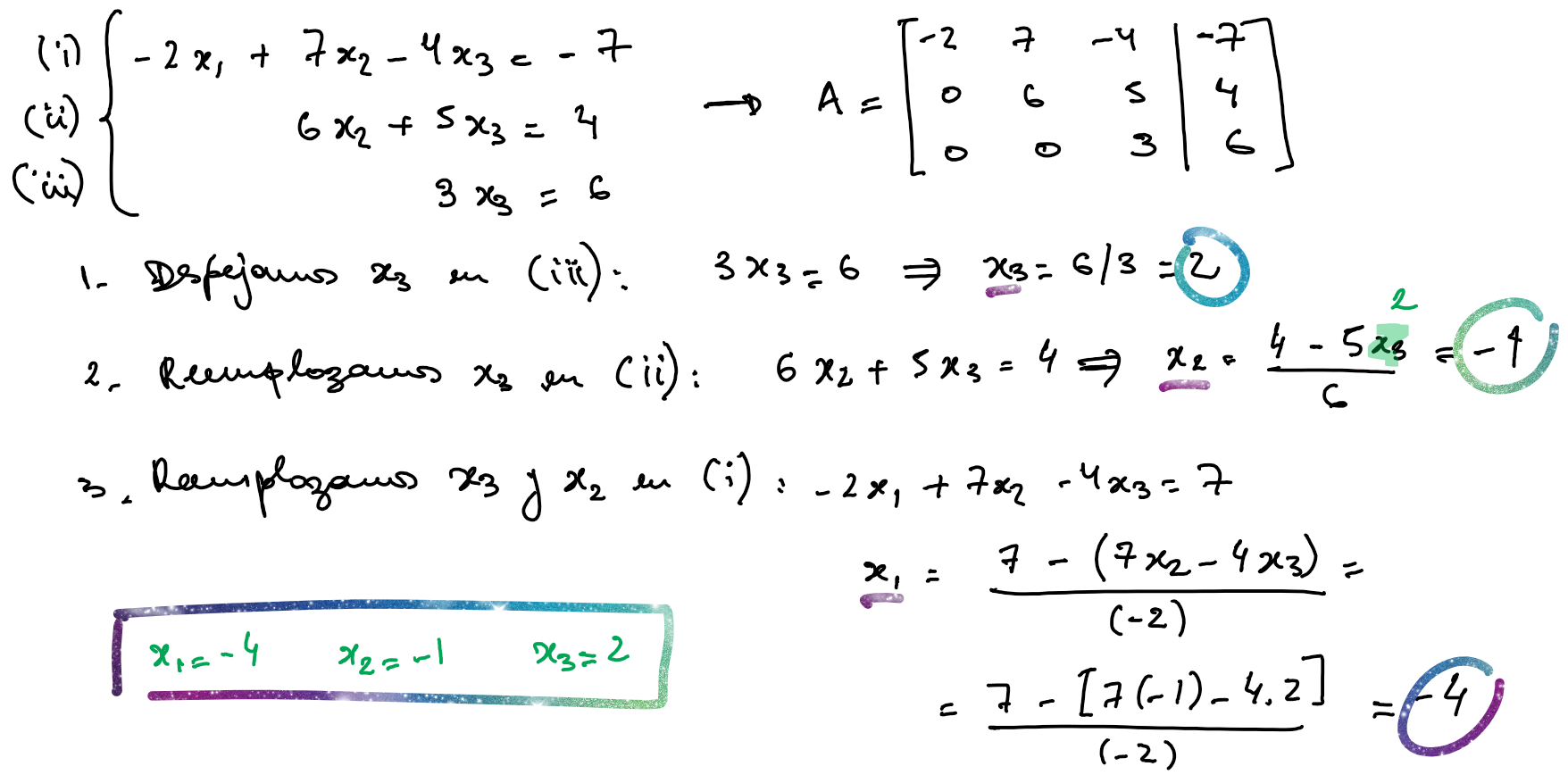

• Hemos encontrado el valor de la última incógnita y fuimos haciendo reemplazos en las ecuaciones desde abajo hacia arriba para encontrar las restantes.

• Esto se conoce como sustitución regresiva o hacia atrás.

• Para poder formalizar este procedimiento que nos resulta natural y así estar en condiciones para implementarlo computacionalmente, tenemos que encontrar una fórmula que exprese sin ambigüedad cómo hacer todos esos cálculos.

• De manera genera, vamos a considerar que la matriz \(\mathbf{A}\) es triangular superior:

  \[ \begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ 0 & a_{22} & a_{23} & \cdots & a_{2n} \\ 0 & 0 & a_{33} & \cdots & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & a_{nn} \end{bmatrix} \times \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix} \]

• La solución de \(x_n\) es inmediata y a partir de ella se encuentran las restantes en orden inverso \(x_{n-1}, \cdots, x_1\), aplicando el algoritmo de sustitución regresiva:

\[ x_n = \frac{b_n}{a_{nn}} \text{ y } x_k = \frac{b_k - \sum_{j = k+1}^{n}a_{kj}x_j}{a_{kk}} \quad k = n-1, n-2, \cdots, 1 \]

• Empleando la notación matricial vista, la suma en el algoritmo puede reescribirse como un producto matricial:

\[ \mathbf{x}[n] = \frac{\mathbf{b}[n]}{\mathbf{A}[n,n]} \qquad \mathbf{x}[k] = \frac{\mathbf{b}[k] - \mathbf{A}[k, (k+1):n] \times \mathbf{x}[(k+1):n]}{\mathbf{A}[k,k]} \qquad k = n-1, n-2, \cdots, 1 \]

• Iniciando el vector solución con ceros, \(\mathbf{x} = [0 ~ 0 \cdots 0]\), la expresión anterior se simplifica aún más:

\[ \mathbf{x}[n] = \frac{\mathbf{b}[n]}{\mathbf{A}[n,n]} \qquad \mathbf{x}[k] = \frac{\mathbf{b}[k] - \mathbf{A}[k, ] \times \mathbf{x}}{\mathbf{A}[k,k]} \qquad k = n-1, n-2, \cdots, 1 \]

• Esto nos permite escribir un algoritmo para la implementación de este método:

knitr::include_graphics("Plots/U3/alg1.png")

Ejercicio:

Operar “a mano” de forma matricial siguiendo los pasos del algoritmo para corroborar su funcionamiento con el sistema de ecuaciones del ejemplo.

• Si la matriz \(\mathbf{A}\) es triangular inferior, la obtención de la solución es análoga al caso anterior y el algoritmo recibe el nombre de sustitución hacia adelante o progresiva.

3.2.3 Eliminación gaussiana

• Es un método para resolver un sistema lineal general \(\mathbf{Ax=b}\) de \(n\) ecuaciones con \(n\) incógnitas.
• El objetivo es construir un sistema equivalente donde la matriz de coeficientes sea triangular superior para obtener las soluciones con el algoritmo de sustitución regresiva.
• El método consiste en ir eliminando incógnitas en las ecuaciones de manera sucesiva, aplicando las operaciones entre ecuaciones que producen sistemas equivalentes (repasadas en la intro).
• Ejemplo: resolver el siguiente sistema

\[ \begin{cases} x+2y-z+3t=-8 \\ 2x+2z-t=13 \\ -x+y+z-t=8\\ 3x+3y-z+2t = -1 \end{cases} \quad \mathbf{A}= \begin{bmatrix} 1 & 2 & -1 & 3 \\ 2 & 0 & 2 & -1 \\ -1 & 1 & 1 & -1 \\ 3 & 3 & -1 & 2 \end{bmatrix} \quad \mathbf{x} = \begin{bmatrix} x \\ y \\ z \\ t \end{bmatrix} \quad \mathbf{b} = \begin{bmatrix} -8 \\ 13 \\ 8 \\ -1 \end{bmatrix} \]

• Matriz aumentada:

\[ \begin{bmatrix} \mathbf{A} & \mathbf{b} \end{bmatrix} = \begin{bmatrix} 1 & 2 & -1 & 3 &|& -8\\ 2 & 0 & 2 & -1 &|& 13\\ -1 & 1 & 1 & -1 &|& 8\\ 3 & 3 & -1 & 2 &|& -1 \end{bmatrix} \] “A mano”

• Primero recordemos cómo resolvemos este tipo de sistemas “a mano”. Seguramente nos resulte familiar la aplicación del método de Gauss, representada en la siguiente imagen:

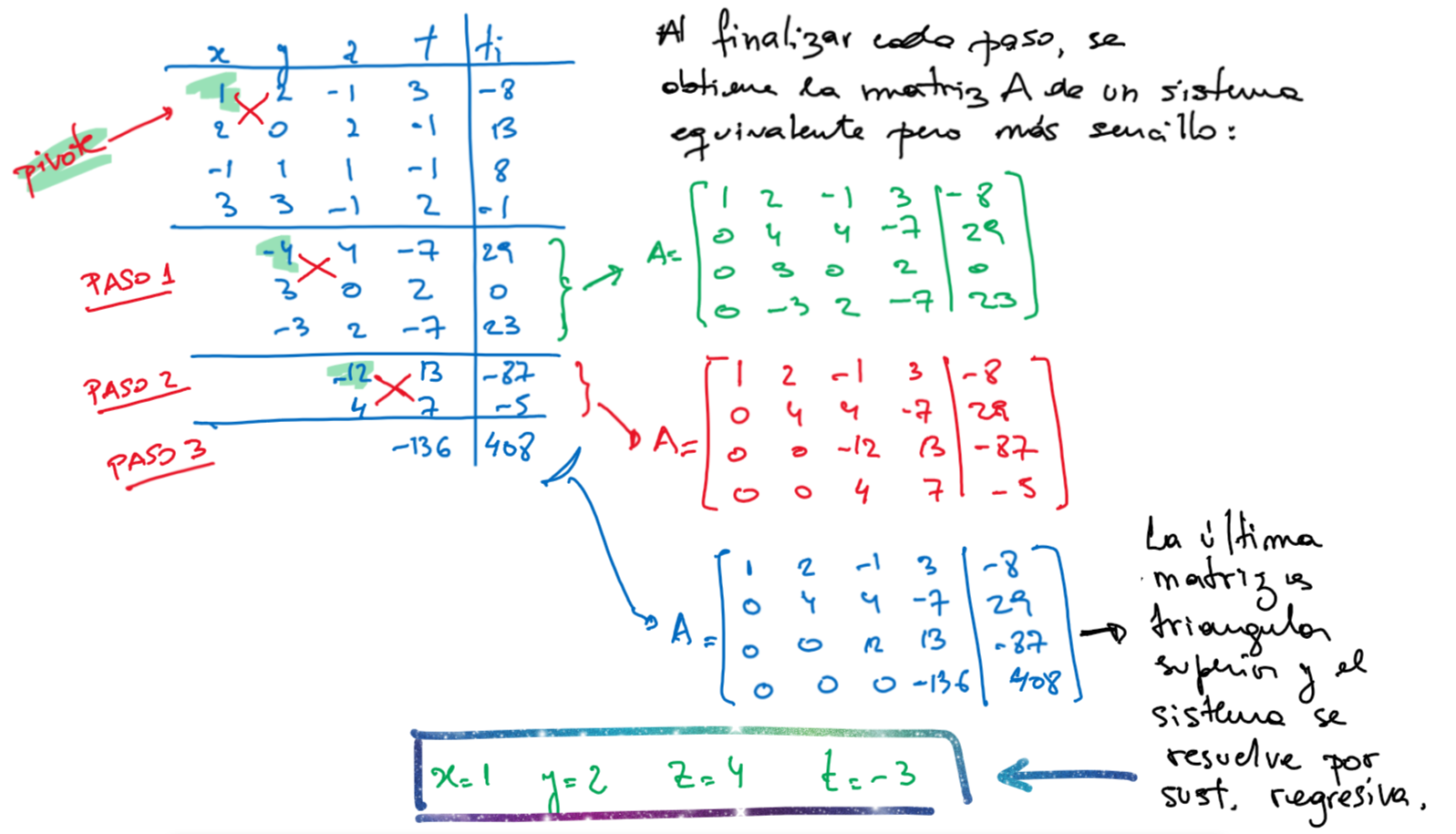
• Como podemos ver, aunque no lo pensemos, al hacer “este por este menos este por este” estamos pasando sucesivamente de un sistema a otro equivalente, con una matriz de coeficientes más sencilla (van apareciendo ceros, es decir, se van elminando incógnitas) hasta llegar a tener una matriz triangular superior, como en el caso anterior.

• Si bien este procedimiento puede ser largo, estamos acostumbrados y no nos presenta ninguna dificultad.

• El desafío surge si tenemos que pensar en una forma de expresarlo formalmente y de hallar fórmulas que puedan ser programadas, de modo que la computadora pueda resolver el sistema por nosotros.

• A continuación vamos a repetir el proceso paso por paso para poder deducir un algoritmo.

Primer paso

• En el primer paso eliminamos la incógnita \(x\) en las ecuaciones 2, 3 y 4, buscando que queden ceros en toda la primera columna excepto en el elemento diagonal.

• Observando con detenimiento, esto se logra realizando reemplazos en las ecuaciones de esta forma:

  \[E_r - m_{r1} \times E_1 \rightarrow E_r \qquad r=2, 3, 4\]

• Los valores \(m_{r1}\) se llaman multiplicadores y se definen como:

  \[m_{r1} = \frac{a_{r1}}{a_{11}}, \quad r = 2, 3, 4\]

• Esta elección de multiplicadores hace que se generen ceros en la primera columna desde la fila 2 hasta la última.

• En este ejemplo, nos quedan:

  \[ m_{21} = \frac{a_{21}}{a_{11}} = 2 \qquad m_{31} = \frac{a_{31}}{a_{11}} = -1 \qquad m_{41} = \frac{a_{41}}{a_{11}} = 3 \]

• Los reemplazos a realizar entonces son:

  \[ \begin{array}{rc} E_2 - 2 \times E_1 & \rightarrow E_2 \\ E_3 - (-1) \times E_1 & \rightarrow E_3 \\ E_4 - 3 \times E_1 & \rightarrow E_4 \end{array} \]

• El elemento \(a_{11}=1\) que está en el denominador de todos los multiplicadores se le dice pivote y a la fila 1 que se usa en los reemplazos se le dice fila pivote.

• El resultado de los reemplazos anteriores es:

  \[ \begin{matrix} \text{pivote} \rightarrow \\ m_{21} = 2 \\ m_{31} = -1 \\ m_{41} = 3 \end{matrix} \begin{bmatrix} 1 & 2 & -1 & 3 &|& -8\\ 2 & 0 & 2 & -1 &|& 13\\ -1 & 1 & 1 & -1 &|& 8\\ 3 & 3 & -1 & 2 &|& -1 \end{bmatrix} \implies \begin{bmatrix} 1 & 2 & -1 & 3 &|& -8\\ 0 & -4 & 4 & -7 &|& 29\\ 0 & 3 & 0 & 2 &|& 0\\ 0 & -3 & 2 & -7 &|& 23 \end{bmatrix} \]

Segundo paso

• En el segundo paso, eliminamos la incógnita \(y\) en las ecuaciones 3 y 4.

• La fila pivote pasa a ser la segunda y el pivote es \(a_{22}=-4\).

• Los multiplicadores son \(m_{r2}=a_{r2}/a_{22}\), \(r=3,4\):

  \[ m_{32} = \frac{a_{32}}{a_{22}} = -3/4 \qquad m_{42} = \frac{a_{42}}{a_{22}} = 3/4 \]

  dando lugar a los reemplazos:

  \[ \begin{array}{rc} E_3 - (-3/4) \times E_2 & \rightarrow E_3 \\ E_4 - 3/4 \times E_2 & \rightarrow E_4 \end{array} \]

• El resultado es:

\[ \begin{matrix} \\ \text{pivote} \rightarrow \\ m_{32} = -3/4 \\ m_{42} = 3/4 \end{matrix} \begin{bmatrix} 1 & 2 & -1 & 3 &|& -8\\ 0 & -4 & 4 & -7 &|& 29\\ 0 & 3 & 0 & 2 &|& 0\\ 0 & -3 & 2 & -7 &|& 23 \end{bmatrix} \implies \begin{bmatrix} 1 & 2 & -1 & 3 &|& -8\\ 0 & -4 & 4 & -7 &|& 29\\ 0 & 0 & 3 & -13/4 &|& 87/4\\ 0 & 0 & -1 & -7/4 &|& 5/4 \end{bmatrix} \]

Tercer paso

• Finalmente, eliminamos la incógnita \(z\) en la última ecuación.

• La fila pivote es la 3º y el pivote es \(a_{33}=3\).

• El multiplicador es \(m_{43}=a_{43}/a_{33}=-1/3\).

• El reemplazo a realizar es:

  \[E_4 - (-1/3) \times E_3 \rightarrow E_4\]

• El resultado es:

\[ \begin{matrix} \\ \\ \text{pivote} \rightarrow \\ m_{43} = -1/3 \end{matrix} \begin{bmatrix} 1 & 2 & -1 & 3 &|& -8\\ 0 & -4 & 4 & -7 &|& 29\\ 0 & 0 & 3 & -13/4 &|& 87/4\\ 0 & 0 & -1 & -7/4 &|& 5/4 \end{bmatrix} \implies \begin{bmatrix} 1 & 2 & -1 & 3 &|& -8\\ 0 & -4 & 4 & -7 &|& 29\\ 0 & 0 & 3 & -13/4 &|& 87/4\\ 0 & 0 & 0 & -17/6 &|& 17/2 \end{bmatrix} \]

• Hemos llegado a un sistema equivalente cuya matriz de coeficientes es triangular superior, en el que aplicamos el algoritmo de sustitución regresiva:

  \[ \left\{ \begin{aligned} x+2y-z-3t &=-8 \cr -4y+4z-7t &=29\cr 3z-13/4t &=87/4\cr -17/6t &=17/2 \end{aligned} \right. \implies \left\{ \begin{aligned} x &= 1\\ y &= 2\\ z &= 4\\ t &= -3 \end{aligned} \right. \]

• Esta matriz triangular es algo diferente a la que obtuvimos cuando hicimos las cuentas con el “cuadrito” de Gauss a mano, pero es equivalente (si prestamos atención, las filas que son distintas en realidad son los mismos valores multiplicados todos por una constante).

• La ventaja de haber hecho los cálculos en términos de multiplicadores y reemplazos de filas, es que ahora tenemos un sistema para crear un algoritmo y poder programarlo.

• Para cada fila \(q\) desde \(1\) hasta \(n-1\) y luego para cada fila \(r\) desde \(q+1\) hasta \(n\), hay que hacer los reemplazos:

  \[ m_{rq} = \frac{a_{rq}}{a_{qq}} \qquad E_r - m_{rq} \times E_q \rightarrow E_r \qquad q=1,...,n-1 \qquad r = q+1, ..., n \]

• El algoritmo resulta ser:

knitr::include_graphics("Plots/U3/alg2.png")

3.2.4 Eliminación gaussiana con estrategias de pivoteo

3.2.4.1 Pivoteo trivial

• En el algoritmo anterior es necesario que los pivotes \(a_{qq} \neq 0 ~\forall q\).

• Si en uno de los pasos encontramos un \(a_{qq} = 0\), debemos intercambiar la \(q\)-ésima fila por una cualquiera de las siguientes, por ejemplo la fila \(k\), en la que \(a_{kq} \neq 0, k>q\).

• Esta estrategia para hallar un pivote no nulo se llama pivoteo trivial.

• Ejemplo: verificar “a mano” que con el siguiente sistema, si seguimos el algoritmo anterior, incurrimos en este problema. En cambio, si seguimos el algoritmo con pivoteo trivial llegamos a la solución.

  \[ \begin{cases} x-2y+z=-4 \\ -2x+4y-3z=3 \\ x-3y-4z=-1 \end{cases} \]

3.2.4.1.1 Estrategias de pivoteo para reducir los errores de redondeo

• Como ya sabemos, dado que las computadoras usan una aritmética cuya precisión está fijada de antemano, es posible que cada vez que se realice una operación aritmética se introduzca un pequeño error de redondeo.
• En la resolución de ecuaciones por eliminación gaussiana, un adecuado reordenamiento de las filas en el momento indicado puede reducir notablemente los errores cometidos.
• Por ejemplo, se puede mostrar cómo buscar en cada paso un multiplicador de menor magnitud (es decir, un pivote de mayor magnitud) mejora la precisión de los resultados.
• Por eso, existen estrategias de pivoteo que no solamente hacen intercambio de filas cuando se tiene un pivote nulo, si no cuando se detecta que un reordenamiento puede reducir el error de redondeo.

Pivoteo parcial

• Para reducir la propagación de los errores de redondeo, antes de comenzar una nueva ronda de reemplazos con el pivote \(a_{qq}\) se evalúa si debajo en la misma columna hay algún elemento con mayor valor absoluto y en ese caso se intercambian las respectivas filas.
• Es decir, se busca si existe \(r\) tal que \(|a_{rq}| > |a_{qq}|,\quad r>q\) para luego intercambiar las filas \(q\) y \(r\).
• Este proceso suele conservar las magnitudes relativas de los elementos de la matriz triangular superior en el mismo orden de magnitud que las de los coeficientes de la matriz original.
• Ver ejemplos 1 y 2 de las páginas 280 y 281.

Pivoteo parcial escalado

• Reduce aún más los efectos de la propagación de los errores.

• Se elige el elemento de la columna \(q\)-ésima, en o por debajo de la diagonal principal, que tiene mayor tamaño relativo con respecto al resto de los elementos de su fila.

• Antes de definir el multiplicador y hacer las operaciones correspondientes, en cada paso se debe:

  1. Buscar el máximo valor absoluto en cada fila:

  \[ s_r = max\{|a_{rq}|, |a_{r,q+1}|, \cdots, |a_{rn}| \} \quad r = q, q+1, \cdots, n \]

  2. Elegir como fila pivote a la que tenga el mayor valor de \(\frac{|a_{rq}|}{s_r}\), \(r = q, q+1, \cdots, n\).
  3. Intercambiar la fila \(q\) con la fila hallada en el punto anterior.

• Ver los ejemplos bajo el título “Ilustración” de las páginas 283 y 284.

3.2.4.2 Algoritmos

• En el siguiente algoritmo se detalla la sistematización necesaria para implementar las tres estrategias de pivoteo mencionadas.
• No se pedirá su programación, se puede usar la función provista.
• Se sugiere la lectura tanto del algoritmo como de la función para distinguir cómo son aplicadas las estrategias.

3.2.5 Método de eliminación de Gauss-Jordan

• Ya vimos que el método de Gauss transforma la matriz de coeficientes \(\mathbf{A}\) en una matriz triangular superior, haciendo estos reemplazos:

  \[ m_{rq} = \frac{a_{rq}}{a_{qq}} \qquad E_r - m_{rq} \times E_q \rightarrow E_r \qquad q=1,...,n-1 \qquad r = q+1, ..., n \]

• El método de Gauss-Jordan transforma \(\mathbf{A}\) hasta obtener la matriz identidad.

• Los multiplicadores se definen de la misma forma, pero en cada paso \(q\) se sustituyen todas las filas, no sólo las filas posteriores a la fila \(q\).

• Para cada fila \(q\) desde \(1\) hasta \(n-1\) y luego para cada fila \(r\) desde \(1\) hasta \(n\), hay que hacer los reemplazos:

  \[ \text{Si } r \neq q:\, m_{rq} = \frac{a_{rq}}{a_{qq}} \qquad E_r - m_{rq} \times E_q \rightarrow E_r \]

  \[ \text{Si } r = q:\,E_r /a_{rr} \rightarrow E_r \]

• Trabajando de esta forma, además de resolver el sistema se puede hallar fácilmente la inversa de \(\mathbf{A}\).

• Para esto hay que concatenar a la derecha de la matriz aumentada una matriz identidad de orden \(n\).

• Cuando en la submatriz izquierda se llega a la matriz identidad, en el centro habrá quedado el vector solución y a su derecha la matriz inversa.

• Retomemos el último ejemplo para resolver el sistema mediante Gauss-Jordan y, de paso, obtener \(\mathbf{A}^{-1}\).

\[ \begin{bmatrix} 1 & 2 & -1 & 3 &|& -8\\ 2 & 0 & 2 & -1 &|& 13\\ -1 & 1 & 1 & -1 &|& 8\\ 3 & 3 & -1 & 2 &|& -1 \end{bmatrix} \]

• Agregamos la matriz identidad a su derecha:

\[ \begin{bmatrix} 1 & 2 & -1 & 3 &|& -8 &|& 1 & 0 & 0 & 0\\ 2 & 0 & 2 & -1 &|& 13 &|& 0 & 1 & 0 & 0 \\ -1 & 1 & 1 & -1 &|& 8 &|& 0 & 0 & 1 & 0\\ 3 & 3 & -1 & 2 &|& -1 &|& 0 & 0 & 0 & 1 \end{bmatrix} \]

• Definimos los multiplicadores y aplicamos las sustituciones:

Paso 1

\[ \begin{matrix} E_2 - 2 E_1 \rightarrow E_2\\ E_3 + E_1 \rightarrow E_3 \\ E_4 - 3 E_1 \rightarrow E_4 \\ E_1 / 1 \rightarrow E_1 \end{matrix} \implies \begin{bmatrix} 1 & 2 & -1 & 3 &|& -8 &|& 1 & 0 & 0 & 0\\ 0 & -4 & 4 & -7 &|& 29 &|& -2 & 1 & 0 & 0\\ 0 & 3 & 0 & 2 &|& 0 &|& 1 & 0 & 1 & 0\\ 0 & -3 & 2 & -7 &|& 23 &|& -3 & 0 & 0 & 1 \end{bmatrix} \]

Paso 2

\[ \begin{matrix} E_1 + 1/2 E_2 \rightarrow E_1\\ E_3 + 3/4 E_2 \rightarrow E_3 \\ E_4 - 3/4 E_2 \rightarrow E_4 \\ E_2 / (-4) \rightarrow E_2 \end{matrix} \implies \begin{bmatrix} 1 & 0 & 1 & -1/2 &|& 13/2 &|& 0 & 1/2 & 0 & 0\\ 0 & 1 & -1 & 7/4 &|& -29/4 &|& 1/2 & -1/4 & 0 & 0\\ 0 & 0 & 3 & -13/4 &|& 87/4 &|& -1/2 & 3/4 & 1 & 0\\ 0 & 0 & -1 & -7/4 &|& 5/4 &|& -3/2 & -3/4 & 0 & 1 \end{bmatrix} \]

Paso 3

\[ \begin{matrix} E_1 - 1/3 E_3 \rightarrow E_1\\ E_2 + 1/3 E_3 \rightarrow E_2 \\ E_4 + 1/3 E_3 \rightarrow E_4 \\ E_3 / 3 \rightarrow E_3 \end{matrix} \implies \begin{bmatrix} 1 & 0 & 0 & 7/12 &|& -3/4 &|& 1/6 & 1/4 & -1/3 & 0\\ 0 & 1 & 0 & 2/3 &|& 0 &|& 1/3 & 0 & 1/3 & 0\\ 0 & 0 & 1 & -13/12 &|& 29/4 &|& -1/6 & 1/4 & 1/3 & 0\\ 0 & 0 & 0 & -17/6 &|& 17/2 &|& -5/3 & -1/2 & 1/3 & 1 \end{bmatrix} \]

Paso 4

\[ \begin{matrix} E_1 + 7/34 E_4 \rightarrow E_1\\ E_2 + 4/17 E_4 \rightarrow E_2 \\ E_3 - 13/34 E_4 \rightarrow E_3 \\ E_4 / (-17/6) \rightarrow E_4 \end{matrix} \implies \begin{bmatrix} 1 & 0 & 0 & 0 &|& 1 &|& -3/17 & 5/34 & -9/34 & 7/34\\ 0 & 1 & 0 & 0 &|& 2 &|& -2/17 & -1/17 & 7/17 & 4/17\\ 0 & 0 & 1 & 0 &|& 4 &|& 8/17 & 15/34 & 7/34 & -13/34\\ 0 & 0 & 0 & 1 &|& -3 &|& 10/17 & 3/17 & -2/17 & -6/17 \end{bmatrix} \]

• En el la columna central tenemos la solución del sistema: \(x=1\), \(y=2\), \(z=4\) y \(t=-3\) y en la submatriz de la derecha, la inversa de \(\mathbf{A}\):

\[ \mathbf{A}^{-1} = \begin{bmatrix} -3/17 & 5/34 & -9/34 & 7/34\\ -2/17 & -1/17 & 7/17 & 4/17\\ 8/17 & 15/34 & 7/34 & -13/34\\ 10/17 & 3/17 & -2/17 & -6/17 \end{bmatrix} \]

• ¿Por qué este procedimiento nos devuelve la inversa de la matriz de coeficientes?

• Recordar que la inversa de \(\mathbf{A}\) es aquella matriz \(\mathbf{A}^{-1}\) que verifica \(\mathbf{AA}^{-1} =\mathbf{A}^{-1}\mathbf{A}=\mathbf{I}\)

• Entonces si queremos hallar la matriz \(\mathbf{A}^{-1}\):

  \[ \mathbf{A}= \begin{bmatrix} 1 & 2 & -1 & 3 \\ 2 & 0 & 2 & -1 \\ -1 & 1 & 1 & -1 \\ 3 & 3 & -1 & 2 \end{bmatrix} \qquad \mathbf{A}^{-1} = \begin{bmatrix} c_{11} & c_{12} & c_{13} & c_{14} \\ c_{21} & c_{22} & c_{23} & c_{24} \\ c_{31} & c_{32} & c_{33} & c_{34} \\ c_{41} & c_{42} & c_{43} & c_{44} \end{bmatrix} \]

  podemos plantear el siguiente producto matricial:

  \[ \begin{bmatrix} 1 & 2 & -1 & 3 \\ 2 & 0 & 2 & -1 \\ -1 & 1 & 1 & -1 \\ 3 & 3 & -1 & 2 \end{bmatrix} \times \begin{bmatrix} c_{11} & c_{12} & c_{13} & c_{14} \\ c_{21} & c_{22} & c_{23} & c_{24} \\ c_{31} & c_{32} & c_{33} & c_{34} \\ c_{41} & c_{42} & c_{43} & c_{44} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

  que da lugar a cuatro sistemas de ecuaciones con la misma matriz de coeficientes, pero distintos vectores de términos independientes, cada uno de los cuales es una columna de la matriz identidad:

  \[ \begin{bmatrix} c_{11}+2c_{21}-c_{31}+3c_{41} & c_{12}+2c_{22}-c_{32}+3c_{42} & c_{13}+2c_{23}-c_{33}+3c_{43} & c_{14}+2c_{24}-c_{34}+3c_{44} \\ 2c_{11}+2c_{31}-c_{41} & 2c_{12}+2c_{32}-c_{42} & 2c_{13}+2c_{33}-c_{43} & 2c_{14}+2c_{34}-c_{44} \\ -c_{11}+c_{21}+c_{31}-c_{41} & -c_{12}+c_{22}+c_{32}-c_{42} & -c_{13}+c_{23}+c_{33}-c_{43} & -c_{14}+c_{24}+c_{34}-c_{44} \\ 3c_{11}+3c_{21}-c_{31}+2c_{41} & 3c_{12}+3c_{22}-c_{32}+2c_{42} & 3c_{13}+3c_{23}-c_{33}+2c_{43} & 3c_{14}+3c_{24}-c_{34}+2c_{44} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

  \[ \begin{cases} c_{11}+2c_{21}-c_{31}+3c_{41}=1 \\ 2c_{11}+2c_{31}-c_{41} =0 \\ -c_{11}+c_{21}+c_{31}-c_{41} =0 \\ 3c_{11}+3c_{21}-c_{31}+2c_{41}= 0 \end{cases} \quad \begin{cases} c_{12}+2c_{22}-c_{32}+3c_{42}=0 \\ 2c_{12}+2c_{32}-c_{42} =1 \\ -c_{12}+c_{22}+c_{32}-c_{42} =0 \\ 3c_{12}+3c_{22}-c_{32}+2c_{42}= 0 \end{cases} \quad \begin{cases} c_{13}+2c_{23}-c_{33}+3c_{43}=0 \\ 2c_{13}+2c_{33}-c_{43} =0 \\ -c_{13}+c_{23}+c_{33}-c_{43} =1 \\ 3c_{13}+3c_{23}-c_{33}+2c_{43}= 0 \end{cases} \quad \begin{cases} c_{14}+2c_{24}-c_{34}+3c_{44}=0 \\ 2c_{14}+2c_{34}-c_{44} =0 \\ -c_{14}+c_{24}+c_{34}-c_{44} =0 \\ 3c_{14}+3c_{24}-c_{34}+2c_{44}= 1 \end{cases} \]

• Al agregar la matriz identidad en la matriz aumentada, lo que estamos haciendo es resolver simultáneamente 5 sistemas de ecuaciones: el original y los 4 que nos permiten encontrar las columnas de la matriz inversa de \(\mathbf{A}\).

• A continuación podemos ver el algoritmo de Gauss-Jordan. Se provee también la función de Python que lo implementa:

3.2.6 Factorización LU

Definición: En álgebra lineal la factorización de una matriz es la descomposición de la misma como producto de dos o más matrices que toman una forma especificada.

• Las factorizaciones de las matrices se utilizan para facilitar el cálculo de diversos elementos como determinantes e inversas y para optimizar algoritmos.

• La factorización LU se obtiene cuando se expresa a una matriz cuadrada \(\mathbf{A}\) como el producto entre una matriz triangular inferior \(\mathbf{L}\) y una matriz triangular superior \(\mathbf{U}\), es decir, \(\mathbf{A} = \mathbf{L} \mathbf{U}\).

• Si bien existe más de una forma de encontrar la descomposición LU de una matriz \(\mathbf{A}\), la misma se puede obtener fácilmente aprovechando los cálculos que se realizan con el método de eliminación gaussiana para resolver un sistema de la forma \(\mathbf{Ax} = \mathbf{b}\).

• Recordemos el ejemplo visto en la sección sobre eliminación gaussiana.

\[ \begin{cases} x+2y-z+3t=-8 \\ 2x+2z-t=13 \\ -x+y+z-t=8\\ 3x+3y-z+2t = -1 \end{cases} \quad \mathbf{A}= \begin{bmatrix} 1 & 2 & -1 & 3 \\ 2 & 0 & 2 & -1 \\ -1 & 1 & 1 & -1 \\ 3 & 3 & -1 & 2 \end{bmatrix} \quad \mathbf{x} = \begin{bmatrix} x \\ y \\ z \\ t \end{bmatrix} \quad \mathbf{b} = \begin{bmatrix} -8 \\ 13 \\ 8 \\ -1 \end{bmatrix} \]

• La factorización LU de la matriz \(\mathbf{A}\) se obtiene al considerar como \(\mathbf{U}\) a la matriz triangular superior que obtuvimos al finalizar la eliminación gaussiana y al crear \(\mathbf{L}\) con los multiplicadores acomodados como se indica a continuación:

\[ \mathbf{L}= \begin{bmatrix} 1 & 0 & 0 & 0 \\ m_{21} & 1 & 0 & 0 \\ m_{31} & m_{32} & 1 & 0 \\ m_{41} & m_{42} & m_{43} & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 2 & 1 & 0 & 0 \\ -1 & -3/4 & 1 & 0 \\ 3 & 3/4 & -1/3 & 1 \end{bmatrix} \qquad \mathbf{U}= \begin{bmatrix} 1 & 2 & -1 & 3 \\ 0 & -4 & 4 & -7 \\ 0 & 0 & 3 & -13/4 \\ 0 & 0 & 0 & -17/6 \end{bmatrix} \]

• Podemos verificar estos cálculos definiendo estas matrices y encontrando que su producto es igual a \(\mathbf{A}\).

3.2.6.1 Usos de la factorización LU

• Una vez encontrada la factorización, esta se puede emplear para facilitar el cálculo de determinantes e inversas y también para resolver otros sistemas del tipo \(\mathbf{Ax} = \mathbf{b}\), con la misma \(\mathbf{A}\) pero cualquier \(\mathbf{b}\).

a. Uso de LU para resolver sistemas de ecuaciones lineales

• Sea \(\mathbf{Ax} = \mathbf{b}\) un sistema lineal que debe resolverse para \(\mathbf{x}\) y supongamos que contamos con la factorización LU de \(\mathbf{A}\) de modo que \(\mathbf{A}\): \(\mathbf{A} = \mathbf{LU}\).

• La solución \(\mathbf{x}\) se encuentra con estos dos pasos:

  1. Resolver el sistema \(\mathbf{Ly} = \mathbf{b}\), donde \(\mathbf{y}\) es el vector de incógnitas. Siendo \(\mathbf{L}\) triangular inferior, este sistema se resuelve fácilmente mediante sustitución hacia adelante.
  2. Resolver el sistema \(\mathbf{Ux} = \mathbf{y}\), donde \(\mathbf{y}\) es el vector obtenido en el punto anterior. Siendo \(\mathbf{U}\) triangular superior, este sistema se resuelve fácilmente mediante sustitución hacia atrás.

• Como se puede ver, los dos pasos consisten resolver sistemas de ecuaciones con matrices de coeficientes triangulares, lo cual es sencillo y no requiere de la implementación de eliminación gaussiana (de todos modos, se necesita aplicar eliminación gaussiana o algún otro proceso para obtener la factorización LU en primer lugar).

• Sin embargo, este procedimiento se puede aplicar para resolver el sistema múltiples veces para diferentes \(\mathbf{b}\). Aplicar eliminación gaussiana una vez para obtener la factorización LU y luego emplearla en la solución de cada sistema es más eficiente que aplicar siempre eliminación gaussiana para cada caso.

• Se dice que las matrices \(\mathbf{L}\) y \(\mathbf{U}\) representan en sí mismas el proceso de eliminación gaussiana.

• Ejemplo: resolver el sistema \(\mathbf{Ax} = \mathbf{b}\) con \(\mathbf{b}^t =[-8 \quad 13 \quad 8 \quad -1]\) a partir de la descomposición LU dada por:

  \[ \mathbf{L}= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 2 & 1 & 0 & 0 \\ -1 & -3/4 & 1 & 0 \\ 3 & 3/4 & -1/3 & 1 \end{bmatrix} \qquad \mathbf{U}= \begin{bmatrix} 1 & 2 & -1 & 3 \\ 0 & -4 & 4 & -7 \\ 0 & 0 & 3 & -13/4 \\ 0 & 0 & 0 & -17/6 \end{bmatrix} \]

b. Uso de LU para calcular la inversa de \(\mathbf{A}\)

• La inversa de \(\mathbf{A}\) se puede obtener como \(\mathbf{A}^{-1} = \mathbf{U}^{-1}\mathbf{L}^{-1}\).
• O también se pueden aplicar los dos pasos anteriores para resolver \(n\) veces el sistema \(\mathbf{Ax} = \mathbf{b}\), haciendo que \(\mathbf{b}\) sea igual a cada una de las columnas de la matriz identidad en cada oportunidad (cada vez \(x\) nos dará una columna de \(\mathbf{A}^{-1}\)).
• Estas formas no son más eficientes que el método tradicional de hallar la inversa de una matriz.

c. Uso de LU para calcular el determinante de \(\mathbf{A}\)

• \(det(\mathbf{A}) = det(\mathbf{L}) det(\mathbf{U})\).
• El determinante de una matriz triangular se obtiene fácilmente como el producto de los elementos diagonales.

3.2.6.2 Otros detalles

• La factorización LU puede llegar a fallar en algunos casos. Por ejemplo, si la obtenemos a través de la eliminación gaussiana, no podríamos completarla cuando algún pivote es cero.
• Así como en la eliminación gaussiana aplicamos pivoteo para evitar ese problema, en el proceso de factorización LU intercambiar el orden de las filas de la matriz también es la solución.
• De hecho, se demuestra que toda matriz cuadrada admite una factorización LU si previamente se reordenan convenientemente sus filas.
• El reordenamiento de filas se representa matemáticamente a través de una matriz \(\mathbf{P}\) de unos y ceros que premultiplicada a \(\mathbf{A}\) produce el efecto de intercambiar filas. Esta matriz se llama matriz de permutación. Luego, toda matriz cuadrada admite una factorización LU del tipo \(\mathbf{PA} = \mathbf{L} \mathbf{U}\) (también llamada factorización PLU).
• La forma vista para obtener de la factorización LU siguiendo los pasos de la eliminación gaussiana recibe el nombre de método de Doolittle y como resultado la matriz \(\mathbf{L}\) tiene unos en su diagonal.
• Otro método que resulta en que la matriz \(\mathbf{U}\) sea la que tenga unos en la diagonal se llama método de Crout.
• La factorización de Cholesky es un caso particular de la factorización LU que se aplica a matrices semidefinidas positivas y que resulta en que \(\mathbf{U} = \mathbf{L}^t\), es decir, \(\mathbf{A} = \mathbf{L} \mathbf{L}^t\).

3.3 Métodos Aproximados o Iterativos

• En esta sección describimos los métodos iterativos de Jacobi y de Gauss-Seidel para resolver sistemas de ecuaciones lineales.
• Una técnica iterativa para resolver el sistema lineal \(\mathbf{Ax} = \mathbf{b}\) inicia con una aproximación \(\mathbf{x}^{(0)}\) para la solución \(\mathbf{x}\) y genera una sucesión de vectores \(\{\mathbf{x}^{(k)}\}_{k=0}^{\infty}\) que convergen a \(\mathbf{x}\).
• Las técnicas iterativas casi nunca se usan para resolver sistemas lineales de dimensiones pequeñas ya que el tiempo requerido para conseguir una precisión suficiente excede el requerido para las técnicas directas, como la eliminación gaussiana.
• Para grandes sistemas con un alto porcentaje de entradas 0, sin embargo, estas técnicas son eficientes en términos tanto de almacenamiento como de cálculo computacional.

3.3.1 Método de Jacobi

• Consideremos el sistema:

  \[ \begin{cases} 4x-y+z=7 \\ 4x-8y+z=-21 \\ -2x+y+5z=15 \end{cases} \implies \begin{cases} x=(7+y-z)/4 \\ y=(21+4x+z)/8 \\ z=(15+2x-y)/5 \end{cases} \]

• Despejar una incógnita en cada ecuación provee expresiones que sugieren la idea de un proceso iterativo.

• Dado un vector de valores iniciales \(\mathbf{x}^{(0)}=(x^{(0)}, y^{(0)}, z^{(0)})\), operar con la siguiente fórmula de recurrencia hasta la convergencia:

  \[ \begin{cases} x^{(k+1)}=(7+y^{(k)}-z^{(k)})/4 \\ y^{(k+1)}=(21+4x^{(k)}+z^{(k)})/8 \\ z^{(k+1)}=(15+2x^{(k)}-y^{(k)})/5 \end{cases} \]

• Por ejemplo, tomando el valor inicial \((1, 2, 2)\), el proceso converge hacia la solución exacta del sistema \((2, 4, 3)\).

• Usando 4 posiciones decimales con redondeo luego de la coma:

  \(k\)	\(x^{(k)}\)	\(y^{(k)}\)	\(z^{(k)}\)
  0	1	2	2
  1	1.7500	3.3750	3.0000
  2	1.8438	3.8750	3.0250
  3	1.9625	3.9250	2.9625
  4	1.9906	3.9766	3.0000
  5	1.9942	3.9953	3.0009
  6	1.9986	3.9972	2.9986
  7	1.9997	3.9991	3.0000
  8	1.9998	3.9999	3.0001
  9	2.0000	3.9999	2.9999
  10	2.0000	4.0000	3.0000

• Observación: no siempre este método converge. Es sensible al ordenamiento de las ecuaciones dentro del sistema.

• Ejemplo: tomamos el mismo sistema de antes pero intercambiamos las filas 1 y 3:

\[ \begin{cases} 4x-y+z=7 \\ 4x-8y+z=-21 \\ -2x+y+5z=15 \end{cases} \implies \begin{cases} -2x+y+5z=15 \\ 4x-8y+z=-21 \\ 4x-y+z=7 \end{cases} \]

\[ \implies \begin{cases} x=(-15+y+5z)/2 \\ y=(21+4x+z)/8 \\ z=7-4x+y \end{cases} \implies \begin{cases} x^{(k+1)}=(-15+y^{(k)}+5z^{(k)})/2 \\ y^{(k+1)}=(21+4x^{(k)}+z^{(k)})/8 \\ z^{(k+1)}=7-4x^{(k)}+y^{(k)} \end{cases} \]

• Tomando el mismo valor inicial \((1, 2, 2)\), esta vez el proceso diverge:

  \(k\)	\(x^{(k)}\)	\(y^{(k)}\)	\(z^{(k)}\)
  0	1	2	2
  1	-1.5000	3.3750	5.0000
  2	6.6875	2.5000	16.3750
  3	34.6875	8.0156	-17.2500
  4	-46.6172	17.8125	-123.7344
  5	-307.9298	-36.1504	211.2813
  6	502.6281	-124.9297	1202.5688
  7	2936.4572	404.2602	-2128.4421
  8	-5126.4752	1204.7983	-11334.5686
  9	-27741.5224	-3977.4337	21717.6991
  10	52298.0309	-11153.4238	106995.6559

• Vamos a desarrollar fórmulas para la expresión general de este método:

\[ \begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2 \\ \vdots \\ a_{j1}x_1 + a_{j2}x_2 + \cdots + a_{jn}x_n = b_j \\ \vdots \\ a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n = b_n \end{cases} \implies \begin{cases} x_1 = \frac{b_1 - a_{12}x_2 - \cdots - a_{1n}x_n}{ a_{11}}\\ x_2 = \frac{b_2 - a_{21}x_1 - a_{23}x_3 - \cdots - a_{2n}x_n}{ a_{22}}\\ \vdots \\ x_j = \frac{b_j - a_{j1}x_1 \cdots - a_{j(j-1)}x_{j-1} - a_{j(j+1)}x_{j+1} - \cdots - a_{jn}x_n}{ a_{jj}}\\ \vdots \\ x_n = \frac{b_n - a_{n1}x_1 - \cdots - a_{n(n-1)}x_{n-1}}{a_{nn}}\\ \end{cases} \]

• A partir de estas expresiones, se plantea el proceso iterativo que arranca con valores iniciales \((x_1^{(0)}, ..., x_n^{(0)})\):

\[ \begin{cases} x_1^{(k+1)} = \frac{b_1 - a_{12}x_2^{(k)} - \cdots - a_{1n}x_n^{(k)}}{ a_{11}}\\ x_2^{(k+1)} = \frac{b_2 - a_{21}x_1^{(k)} - a_{23}x_3^{(k)} - \cdots - a_{2n}x_n^{(k)}}{ a_{22}}\\ \vdots \\ x_j^{(k+1)} = \frac{b_j - a_{j1}x_1^{(k)} \cdots - a_{j(j-1)}x_{j-1}^{(k)} - a_{j(j+1)}x_{j+1}^{(k)} - \cdots - a_{jn}x_n^{(k)}}{ a_{jj}}\\ \vdots \\ x_n^{(k+1)} = \frac{b_n - a_{n1}x_1^{(k)} - \cdots - a_{n(n-1)}x_{n-1}^{(k)}}{a_{nn}}\\ \end{cases} \]

\[ \implies x_j^{(k+1)} = \frac{1}{a_{jj}} \Big[ b_j - \sum_{\substack{i=1 \\ i \neq j}}^{n} a_{ji}x_{j}^{(k)} \Big] \qquad j=1, 2, \cdots n \qquad k=0, 1, 2, \cdots \]

• Lo anterior se puede expresar de forma matricial para simplificar la tarea de programación o para tener una expresión más cómoda a fines de estudiar propiedades teóricas del método.

• Si descomponemos a la matriz \(\mathbf{A}\) como \(\mathbf{A=D+R}\), donde \(\mathbf{D}\) es la matriz diagonal formada con la diagonal de \(\mathbf{A}\) y \(\mathbf{R}\) es igual a \(\mathbf{A}\) excepto en la diagonal donde posee todos ceros, tenemos:

  \[\begin{align*} \mathbf{Ax} &= \mathbf{b} \\ \mathbf{(D+R)x} &= \mathbf{b} \\ \mathbf{Dx} &= \mathbf{b} - \mathbf{Rx} \\ \mathbf{x} &= \mathbf{D}^{-1} (\mathbf{b} - \mathbf{Rx}) \\ \end{align*}\]

• Esto da lugar a la siguiente fórmula de recurrencia, que es equivalente a la vista anteriormente:

  \[ \mathbf{x}^{(k+1)} = \mathbf{D}^{-1} (\mathbf{b} - \mathbf{Rx}^{(k)}) \]

• Requisito: ningún elemento en la diagonal de \(\mathbf{A}\) es cero.

3.3.2 Método de Gauss-Seidel

• Toma la misma idea que Jacobi, pero con una pequeña modificación para acelerar la convergencia.
• La diferencia está en que apenas calcula un nuevo valor de las incógnitas, Gauss-Seidel lo usa inmediatamente en el cálculo de las restantes dentro del mismo paso iterativo, en lugar esperar a la próxima ronda.
• Retomando el ejemplo anterior:

\[ \begin{cases} 4x-y+z=7 \\ 4x-8y+z=-21 \\ -2x+y+5z=15 \end{cases} \implies \begin{cases} x=(7+y-z)/4 \\ y=(21+4x+z)/8 \\ z=(15+2x-y)/5 \end{cases} \stackrel{Jacobi}{\implies} \begin{cases} x^{(k+1)}=(7+y^{(k)}-z^{(k)})/4 \\ y^{(k+1)}=(21+4x^{(k)}+z^{(k)})/8 \\ z^{(k+1)}=(15+2x^{(k)}-y^{(k)})/5 \end{cases} \]

• El proceso iterativo de Gauss-Seidel es:

\[ \begin{cases} x^{(k+1)}=(7+y^{(k)}-z^{(k)})/4 \\ y^{(k+1)}=(21+4x^{(k+1)}+z^{(k)})/8 \\ z^{(k+1)}=(15+2x^{(k+1)}-y^{(k+1)})/5 \end{cases} \]

• Tomando otra vez el valor inicial \((1, 2, 2)\) y operando con 4 posiciones decimales con redondeo luego de la coma:

  Jacobi				Gauss-Seidel
  \(k\)	\(x^{(k)}\)	\(y^{(k)}\)	\(z^{(k)}\)	\(k\)	\(x^{(k)}\)	\(y^{(k)}\)	\(z^{(k)}\)
  0	1	2	2	0	1	2	2
  1	1.7500	3.3750	3.0000	1	1.7500	3.7500	2.9500
  2	1.8438	3.8750	3.0250	2	1.9500	3.9688	2.9862
  3	1.9625	3.9250	2.9625	3	1.9957	3.9961	2.9991
  4	1.9906	3.9766	3.0000	4	1.9993	3.9995	2.9998
  5	1.9942	3.9953	3.0009	5	1.9999	3.9999	3.0000
  6	1.9986	3.9972	2.9986	6	2.0000	4.0000	3.0000
  7	1.9997	3.9991	3.0000
  8	1.9998	3.9999	3.0001
  9	2.0000	3.9999	2.9999
  10	2.0000	4.0000	3.0000

• En general, este método converge más rápidamente que el de Jacobi, pero no siempre es así.

• Existen sistemas lineales para los que el método de Jacobi converge y el de Gauss-Seidel no.

• La expresión general para el método es:

\[ \begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2 \\ \vdots \\ a_{j1}x_1 + a_{j2}x_2 + \cdots + a_{jn}x_n = b_j \\ \vdots \\ a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n = b_n \end{cases} \implies \begin{cases} x_1 = \frac{b_1 - a_{12}x_2 - \cdots - a_{1n}x_n}{ a_{11}}\\ x_2 = \frac{b_2 - a_{21}x_1 - a_{23}x_3 - \cdots - a_{2n}x_n}{ a_{22}}\\ \vdots \\ x_j = \frac{b_j - a_{j1}x_1 \cdots - a_{j(j-1)}x_{j-1} - a_{j(j+1)}x_{j+1} - \cdots - a_{jn}x_n}{ a_{jj}}\\ \vdots \\ x_n = \frac{b_n - a_{n1}x_1 - \cdots - a_{n(n-1)}x_{n-1}}{a_{nn}}\\ \end{cases} \]

• A partir de estas expresiones, se plantea el proceso iterativo que arranca con valores iniciales \((x_1^{(0)}, ..., x_n^{(0)})\):

\[ \begin{cases} x_1^{(k+1)} = \frac{b_1 - a_{12}x_2^{(k)} - \cdots - a_{1n}x_n^{(k)}}{ a_{11}}\\ x_2^{(k+1)} = \frac{b_2 - a_{21}x_1^{(k+1)} - a_{23}x_3^{(k)} - \cdots - a_{2n}x_n^{(k)}}{ a_{22}}\\ \vdots \\ x_j^{(k+1)} = \frac{b_j - a_{j1}x_1^{(k+1)} \cdots - a_{j(j-1)}x_{j-1}^{(k+1)} - a_{j(j+1)}x_{j+1}^{(k)} - \cdots - a_{jn}x_n^{(k)}}{ a_{jj}}\\ \vdots \\ x_n^{(k+1)} = \frac{b_n - a_{n1}x_1^{(k+1)} - \cdots - a_{n(n-1)}x_{n-1}^{(k+1)}}{a_{nn}}\\ \end{cases} \]

\[ \implies x_j^{(k+1)} = \frac{1}{a_{jj}} \Big[ b_j - \sum_{i<j} a_{ji} x_i^{(k+1)} - \sum_{i>j} a_{ji} x_i^{(k)} \Big] \qquad j = 1,...,n \quad k = 0, 1, 2, ... \]

• Para encontrar una expresión matricial, descomponemos a la matriz \(\mathbf{A}\) como \(\mathbf{A=L+U}\), donde \(\mathbf{L}\) es una matriz triangular inferior (incluyendo la diagonal de \(\mathbf{A}\)) y \(\mathbf{U}\) es una matriz triangular superior (con ceros en la diagonal):

  \[\begin{align*} \mathbf{Ax} &= \mathbf{b} \\ \mathbf{(L+U)x} &= \mathbf{b} \\ \mathbf{Lx} &= \mathbf{b} - \mathbf{Ux} \\ \mathbf{x} &= \mathbf{L}^{-1} (\mathbf{b} - \mathbf{Ux}) \\ \end{align*}\]

• Esto da lugar a la siguiente fórmula de recurrencia, que es equivalente a la vista anteriormente:

  \[ \mathbf{x}^{(k+1)} = \mathbf{L}^{-1} (\mathbf{b} - \mathbf{Ux}^{(k)}) \]

• Requisito: ningún elemento en la diagonal de \(\mathbf{A}\) es cero.

3.3.3 Convergencia

Condiciones para la convergencia

• Para establecer una condición de convergencia de estos métodos, necesitamos la siguiente definición:

Definición:

• Se dice que una matriz \(\mathbf{A}\) de orden \(n \times n\) es diagonal dominante cuando cada elemento diagonal es mayor o igual a la suma del resto de los elementos de su fila en valor absoluto:

  \[ |a_{kk}| \geq \sum\limits_{\substack{j=1 \\ j\neq k}}^n |a_{kj}| \quad \forall \,k=1, 2, \cdots, n \]

• Se dice que una matriz \(\mathbf{A}\) de orden \(n \times n\) es estrictamente diagonal dominante cuando cada elemento diagonal es mayor a la suma del resto de los elementos de su fila en valor absoluto:

  \[ |a_{kk}| > \sum\limits_{\substack{j=1 \\ j\neq k}}^n |a_{kj}| \quad \forall \,k=1, 2, \cdots, n \]

• Los sistemas de ecuaciones cuya matriz de coeficiente es estrictamente diagonal dominante poseen algunas ventajas.
• Una matriz estrictamente diagonal dominante es no singular (el sistema es compatible determinado).
• Además, la eliminación gaussiana se puede realizar sin intercambios de fila o columna y los cálculos serán estables respecto al crecimiento de los errores de redondeo.
• Y en particular, para estas matrices está asegurada la convergencia de los métodos iterativos, como lo indica el siguiente teorema:

Teorema: si la matriz \(\mathbf{A}\) es estrictamente diagonal dominante, entonces el sistema lineal \(\mathbf{Ax=b}\) tiene solución única y los procesos iterativos de Jacobi y de Gauss-Seidel convergen hacia la misma cualquiera sea el vector de partida \(\mathbf{x}^{(0)}\).

• Es una condición suficiente pero no necesaria.
• En la práctica, ante un sistema buscamos reordenar las columnas y filas para intentar obtener una matriz con estas características.
• Si no es posible, igualmente buscamos colocar en la diagonal los elementos de mayor valor absoluto, puesto que esto puede favorecer la convergencia.

3.3.3.1 Criterios para detener el proceso iterativo

• Para establecer si los métodos iterativos están convergiendo y así detener el proceso, necesitamos una forma para medir la distancia entre vectores columna \(n\)-dimensionales (es decir, entre dos vectores \(\mathbf{x}^{(k)}\) consecutivos en la iteración).
• Para definir la distancia en \(\mathbb{R}^n\) usamos la noción de norma, que es la generalización del valor absoluto en \(\mathbb{R}\).

Definición: Una norma vectorial en \(\mathbb{R}^n\) es una función \(||\cdot||\) de \(\mathbb{R}^n\) a \(\mathbb{R}\), con las siguientes propiedades:

1. \(||\mathbf{x}|| \geq 0 \quad \forall \, \mathbf{x} \in \mathbb{R}^n\)
2. \(||\mathbf{x}|| = 0 \Leftrightarrow \mathbf{x} = \mathbf{0}\)
3. \(||\alpha \mathbf{x}|| = |\alpha| ||\mathbf{x}|| \quad \forall \, \alpha \in \mathbb{R}, \mathbf{x} \in \mathbb{R}^n\)
4. \(|| \mathbf{x} + \mathbf{y}|| \leq ||\mathbf{x}|| + ||\mathbf{y}|| \quad \forall \, \mathbf{x}, \mathbf{y} \in \mathbb{R}^n\)

• Las siguientes son tres normas ampliamente utilizadas:

  1. Norma \(l_1\): \(||\mathbf{x}||_1 = \sum_{j=1}^n |x_j|\)
  2. Norma \(l_2\) o euclideana: \(||\mathbf{x}||_2 = \sqrt{\mathbf{x}^t\mathbf{x}} = \sqrt{\sum_{j=1}^n x_j^2}\)
  3. Norma \(l_{\infty}\): \(||\mathbf{x}||_{\infty} = \max_{1 \leq j \leq n} |x_j|\)

• La norma de un vector proporciona una medida para la distancia entre un vector arbitrario y el vector cero, de la misma forma en la que el valor absoluto de un nùmero real describe su distancia desde 0.

• De igual forma, la distancia entre dos vectores (que necesitamos para juzgar la convergencia del proceso) está definida como la norma de la diferencia de los vectores, al igual que la distancia entre dos números reales es el valor absoluto de la diferencia.

• Luego, para “comparar” dos vectores sucesivos que aproximan a la solución del sistema, podemos usar las siguientes definiciones de distancias:

  1. Distancia \(l_1\) o de Manhattan:

     \[ ||\mathbf{x}^{(k+1)}-\mathbf{x}^{(k)}||_1 =\sum_{j=1}^n |x_j^{(k+1)} - x_j^{(k)}| \]

  2. Distancia \(l_2\) o euclídea:

     \[||\mathbf{x}^{(k+1)}-\mathbf{x}^{(k)}||_2 = \sqrt{(\mathbf{x}^{(k+1)}-\mathbf{x}^{(k)})^t(\mathbf{x}^{(k+1)}-\mathbf{x}^{(k+1)})} = \sqrt{\sum_{j=1}^n (x_j^{(k+1)} - x_j^{(k)})^2}\]

  3. Distancia \(l_\infty\) o máxima diferencia:

  \[ ||\mathbf{x}^{(k+1)}-\mathbf{x}^{(k)}||_\infty = \max_{j} |x_j^{(k+1)} - x_j^{(k)}| \]

• El proceso iterativo se detiene cuando la distancia elegida entre dos vectores solución consecutivos sea menor a algún valor tan pequeño como se desee, \(\epsilon\).

• Lo más común es emplear la norma \(l_\infty\).

• Siendo semejante a la definición de error relativo, también es usual iterar hasta que:

  \[\frac{||\mathbf{x}^{(k+1)}-\mathbf{x}^{(k)}||}{||\mathbf{x}^{(k+1)}||} < \epsilon\]

• Por último, se debe establecer un número máximo de iteraciones, para detener el proceso cuando el mismo no converge.